
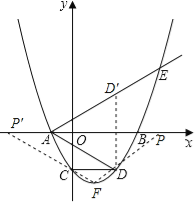
【题目】如图,二次函数y=a(x2-2mx-3m2)(其中a,m为常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B左侧),与y轴交于点C(0,-3),点D在二次函数图象上,且CD∥AB,连AD;过点A作射线AE交二次函数于点E,使AB平分∠DAE.
(1)当a=1时,求点D的坐标;
(2)证明:无论a、m取何值,点E在同一直线上运动;
(3)设该二次函数图象顶点为F,试探究:在x轴上是否存在点P,使以PF、AD、AE为边构成的三角形是以AE为斜边的直角三角形?如果存在,请用含m的代数式表示点P的横坐标,如果不存在,请说明理由.

【答案】(1)D(2,-3);(2)证明见解析;(3)P(-3m,0)或(5m,0).
【解析】试题分析:(1)根据题意将a=1,C(0,﹣3)代入y=a(x2﹣2mx﹣3m2),进而求出m的值,即可得出答案;
(2)首先根据题意表示出A,B,C,D,进而联立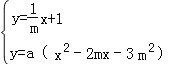 ,求出E点坐标即可得出答案;
,求出E点坐标即可得出答案;
(3)由(2)得:F(m,﹣4)、E(4m,5)、A(﹣m,0)、D(2m,﹣3),再利用PF,AD,AE的关系得出答案.
解:(1)当a=1时,y=a(x2﹣2mx﹣3m2)=x2﹣2mx﹣3m2,
∵与y轴交于点C(0,﹣3),
∴﹣3m2=﹣3,
解得:m=±1,
∵m>0,
∴m=1,
∴抛物线解析式为:y=x2﹣2x﹣3=(x﹣1)2+4,
故抛物线顶点坐标为:D(2,﹣3);
(2)作D关于AB对称的点D′必在AE上,
当y=0,则0=a(x2﹣2mx﹣3m2),
解得:x1=﹣m,x2=3m,
当x=0,y=﹣3am2,
可得:A(﹣m,0)、B(3m,0),C(0,﹣3am2),D(2m,﹣3am2)
∴D′(2m,3am2),
∵抛物线过点C,
∴﹣3am2=﹣3,
则am2=1,
∴直线AD′的解析式为:y=![]() x+1,
x+1,
联立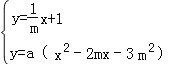 ,整理得x2﹣3mx﹣4m2=0
,整理得x2﹣3mx﹣4m2=0
解得x1=4m,x2=﹣m(舍去)
∴E(4m,5)
∴E在y=5上运动;
(3)由(2)得:F(m,﹣4)、E(4m,5)、A(﹣m,0)、D(2m,﹣3)
设P(b,0)
∴PF2=(m﹣b)2+16,AD2=9m2+9,AE2=25m2+25
∴(m﹣b)2+16+9m2+9=25m2+25,
解得:b1=﹣3m,b2=5m
∴P(﹣3m,0)或(5m,0).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】人体中红细胞的直径约为0.0000077 m,用科学记数法表示数的结果是( )
A. 0.77×10-5 m B. 0.77×10-6 m
C. 7.7×10-5 m D. 7.7×10-6 m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅览室某一书架上原有图书20本,规定每天归还图书为正,借出图书为负,经过两天借阅情况如下:(﹣3,+1),(﹣1,+2),则该书架上现有图书本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
⑴请你补全这个输水管道的圆形截面;
⑵若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(1,0),B(4,0),C(3,3),D(1,4).
(1)描出A、B、C、D、四点的位置,并顺次连接ABCD;
(2)四边形ABCD的面积是________.
(3)把四边形ABCD向左平移5个单位,再向上平移1个单位得到四边形A′B′C′D′,写出点A′、B′、C′、D′的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com