
 如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,求∠B′A′C的大小.
如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,求∠B′A′C的大小. 科目:初中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{13}}{13}$ | D. | $\frac{3\sqrt{13}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
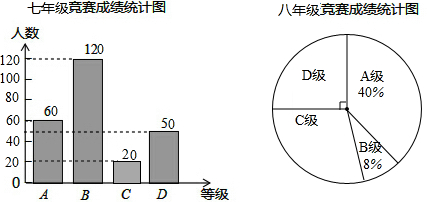
 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com