
【题目】阅读下列材料:
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得y=![]() =4-
=4-![]() x,(x、y为正整数)
x,(x、y为正整数)
∴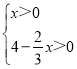 则有0<x<6
则有0<x<6
又y=4-![]() x为正整数,则
x为正整数,则![]() x为正整数.
x为正整数.
从而x=3,代入y=4-![]() ×3=2
×3=2
∴2x+3y=12的正整数解为![]() .
.
利用以上方法解决下列问题:
七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
【答案】有两种购买方案,方案一:购买单价为3元的笔记本5本,单价为5元的钢笔4支;方案二:购买单价为3元的笔记本10本,单价为5元的钢笔1支.
【解析】
设购买单价为3元的笔记本m本,单价为5元的钢笔n支,根据总价=单价×数量,即可得出关于m、n的二元一次方程,结合m、n均为正整数即可求出结论.
设购买单价为3元的笔记本m本,单价为5元的钢笔n支,
根据题意得:3m+5n=35,其中m、n均为正整数,
∴n=![]() =7-
=7-![]() m,
m,
∴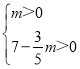 ,
,
解得:0<m<![]() .
.
∵n=7-![]() m为正整数,
m为正整数,
∴![]() m为正整数,即m为5的倍数,
m为正整数,即m为5的倍数,
∴当m=5时,n=4;当m=10时,n=1.
答:有两种购买方案,方案一:购买单价为3元的笔记本5本,单价为5元的钢笔4支;方案二:购买单价为3元的笔记本10本,单价为5元的钢笔1支.


科目:初中数学 来源: 题型:
【题目】如图,如图,抛物线y=x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方的动点,过点M作MN∥y轴交直线BC于点N求线段MN的最大值;(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了4cm.求该摆绳CD的长度.(精确到0.1cm,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块三角形模具的阴影部分已破损.回答下列问题:
(1)只要从模具片中度量出哪些边、角,就可以到店铺加工一块与原来的模具△ABC的形状和大小完全相同的△A′B′C′模具?请简要说明理由.
(2)按尺规作图的要求,在框内正确作出△A′B′C′图形,保留作图痕迹,不写作法和证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
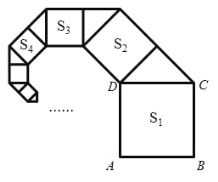
【题目】如图,正方形 ABCD 的边长为1,其面积为 S1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为 S2,…,按此规律继续下去,则 S9的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早上,住在同一小区的小雨、小静两人从小区出发,沿相同的路线步行到学校上学.小雨出发5分钟后,小静才出发,同时小雨发现自己没带手表,于是决定按原速回家拿手表小雨拿到手表后,担心会迟到,于是速度提高了20%,结果比小静早2分钟到校.小雨取手表的时间忽略不计,在整个过程中,小静始终保持匀速运动,小雨提速前后也分别保持匀速运动,如图所示是小雨、小静之间的距离![]() (米)与小雨离开小区的时间
(米)与小雨离开小区的时间![]() (分钟)之间的函数图像,则小区到学校的距离是_______米.
(分钟)之间的函数图像,则小区到学校的距离是_______米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当点P运动到CD上时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com