练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．现定义运算“★”，对于任意实数a、b，都有a★b=a2-a+b，如3★5=32-3+5，若x★2=8，则实数x的值是x1=-2，x2=3．

    分析 根据新定理得到x2-x+2=8，整理得x2-x-6=0，然后利用因式分解法解方程．

    解答 解：∵x★2=8，
    ∴x2-x+2=8，
    即x2-x-6=0，
    （x+2）（x-3）=0，
    x+2=0或x-3=0，
    ∴x1=-2，x2=3．
    故答案为x1=-2，x2=3．

    点评 本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    20．在?ABCD中，∠ABC的平分线交直线AD于点E，且AE=5，ED=2，则?ABCD的周长是24或16．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．【问题情境】如图①，直角三角板ABC中，∠C=90°，AC=BC，将一个用足够长的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上，再将该直角绕点D旋转，并使其两边分别与三角板的AC边、BC边交于P、Q两点．
    【问题探究】
    （1）在旋转过程中，
    ①如图2，当AD=BD时，线段DP、DQ的数量关系是（　　）
    A、DP＜DQ       B、DP=DQ      C、DP＞DQ      D、无法确定
    ②如图3，当AD=2BD时，线段DP、DQ有何数量关系？并说明理由．
    ③根据你对①、②的探究结果，试写出当AD=nBD时，DP、DQ满足的数量关系为DP=nDQ（直接写出结论，不必证明）
    （2）当AD=BD时，若AB=20，连接PQ，设△DPQ的面积为S，在旋转过程中，S是否存在最小值或最大值？若存在，求出最小值或最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．解下列分式方程
    （1）$\frac{2}{x-1}$-1=$\frac{x+1}{x-1}$                      
    （2）$\frac{x+2}{x-2}$=$\frac{x}{x+1}$
    （3）$\frac{3x-5}{x-1}$-$\frac{2x-5}{x-2}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

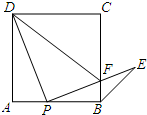    12．如图，点P是正方形ABCD边AB上一点（不与点A，B重合），连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE，PE交边BC于点F，连接BE，DF．
    （1）求证：∠ADP=∠EPB；
    （2）求∠CBE的度数；
    （3）当点P是AB的中点且AB=2，则BF的长为$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．抛一枚均匀的硬币200次，若正面朝上的次数为102次，则正面朝上的频率是0.51，反面朝上的频率是0.49．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．随着车辆的增加，交通违规的现象越来越严重，交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理（速度在30-40含起点值30，不含终点值40），得到其频数及频率如表：
    数据段频数频率
    30-40100.05
    40-5036c
    50-60a0.39
    60-70bd
    70-80200.10
    总计2001
    （1）表中a、b、c、d分别为：a=78； b=56； c=0.18； d=0.28
    （2）补全频数分布直方图；
    （3）如果汽车时速不低于60千米即为违章，则违章车辆共有多少辆？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．将4个数，a，b，c，d排成两行、两列，两边各加一条竖线，记成$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$，定义$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，上述记号叫做二阶行列式，若$|\begin{array}{l}{x+1}&{1-x}\\{1-x}&{x+1}\end{array}|$=8，求$\frac{1}{2}$x[（2x+3）2-（2x-3）2]÷（2x）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如果$\frac{x}{y}$=$\frac{7}{3}$，那么$\frac{x-y}{y}$=$\frac{4}{3}$．

    查看答案和解析>>

    同步练习册答案