
分析 (1)先把给出的式子化成完全平方的形式,再根据非负数的性质即可得出答案;
(2)根据完全平方公式把给出的式子进行整理,即可得出答案;
(3)根据完全平方公式把给出的式子进行整理,即可得出答案.
解答 解:(1)3x2-6x+2
=3(x2-2x)+2
=3(x2-2x+1-1)+2
=3(x-1)2-1,
∵无论x取什么数,都有(x-1)2的值为非负数,
∴(x-1)2的最小值为0,此时x=1,
∴3(x-1)2-1的最小值为-1;
则当x=1时,原多项式的最小值是-1;
(2)同(1)得:4-x2+2x=-(x-1)2+5,
∵无论x取什么数,都有(x-1)2的值为非负数,
∴(x-1)2的最小值为0,此时x=1,
∴-(x-1)2+5的最大值为:-0+5=5,
则当x=1时,原多项式的最大值是5.
(3)同(1)得:x2+2x+y2-4y+9=(x+1)2+(y-2)2+4,
当(x+1)2=0,(y-2)2=0时,多项式x2+2x+y2-4y+9的最小值为4.
点评 此题考查了配方法的应用,用到的知识点是完全平方公式,非负数的性质,解题的关键是把给出的式子化成完全平方的形式.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠EFD=∠C.
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠EFD=∠C. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等边三角形ABC中,D,E分别是AB,AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接DE,CD,EF.
如图,等边三角形ABC中,D,E分别是AB,AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接DE,CD,EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
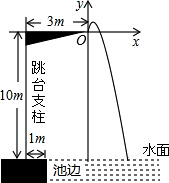 如图,某运动员在2016年里约奥运会10米跳台跳水比赛时,估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为10$\frac{2}{3}$米.
如图,某运动员在2016年里约奥运会10米跳台跳水比赛时,估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为10$\frac{2}{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机正在播放欧洲杯 | |
| B. | 任意画一个三角形,其内角和为360° | |
| C. | 掷一枚质地均匀的骰子,掷出的点数为8 | |
| D. | 平行于同一条直线的两条直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com