【题目】从-3、-1、
、1、3这五个数中，随机抽取一个数，记为a，则关于x的一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为______．
【答案】
．
【解析】
分别求出一次函数图象与坐标轴的交点坐标，可得一次函数y=-x+a的图象与坐标轴围成三角形的面积，再根据概率公式，即可求解．
当a=-3，则y=-x-3，此时图象与x轴交点坐标为：(-3，0)，与y轴交点坐标为：(0，-3)，
故一次函数y=-x+a的图象与坐标轴围成三角形的面积为4.5，不合题意；
当a=3，则y=-x+3，此时图象与x轴交点坐标为：(3，0)，与y轴交点坐标为：(0，3)，
故一次函数y=-x+a的图象与坐标轴围成三角形的面积为4.5，不合题意；
当a=-1、
、1时，一次函数y=-x+a的图象与坐标轴围成三角形的面积分别为：，
，，符合题意，
∴一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为：
．
故答案为：．
科目：初中数学 来源： 题型：
【题目】若方程x2+（2a-1）x+a2=0与方程2x2-（4a+1）x+2a-1=0中至多有一个方程有实数根，则a的取值范围是（ ）
A.a＞
B.a＜-
C.
≤a≤D.a＜-或a＞
查看答案和解析>>
科目：初中数学 来源： 题型：
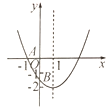
【题目】如图，已知二次函数
的图象与
轴交于点
，与
轴的交点
在
和
之间（不包括这两点），对称轴为直线
.下列结论：①
；②
；③
；④
；⑤
.其中正确的是________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y＝mx2+2mx+n与x轴的一个交点为A（﹣3，0），与y轴的负半轴交于点C．
（1）直接写出抛物线的对称轴，及抛物线与x轴的另一个交点B的坐标；
（2）点C关于x轴的对称点为点D，当点D在以AB为直径的半圆上时，求抛物线的解析式；
（3）在（2）的情况下，在抛物线上是否存在一点P，使BP，BD，AB三条之中，其中一条是另两条所夹角的角平分线？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
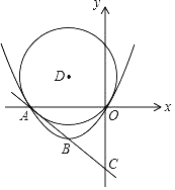
【题目】 已知：直线y=-x-4分别交x、y轴于A、C两点，点B为线段AC的中点，抛物线y=ax2+bx经过A、B两点，
（1）求该抛物线的函数关系式；
（2）以点B关于x轴的对称点D为圆心，以OD为半径作⊙D，连结AD、CD，问在抛物线上是否存在点P，使S△ACP=2S△ACD？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由；
（3）在（2）的条件下，若E为⊙D上一动点(不与A、O重合)，连结AE、OE，问在x轴上是否存在点Q，使∠ACQ：∠AEO=2：3？若存在，请求出所有满足条件的点Q的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
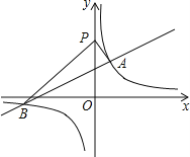
【题目】如图，一次函数y=kx+2的图象与反比例函数y=
的图象交于A、B两点，其中A点坐标为（2，3）．
（1）求两个函数的表达式；
（2）点P是y轴上的一个动点，当∠APB为直角时，求P点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠MAN＝30°，点O为边AN上一点，以O为圆心，4为半径
作⊙O交AN于D、E两点．
⑴ 当⊙O与AM相切时，求AD的长；
⑵ 如果AD＝2，那么AM与⊙O又会有怎样的位置关系？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在矩形ABCD中，G为AD上一点，连接BG，CG，作CE⊥BG于点E，连接ED交GC于点F．
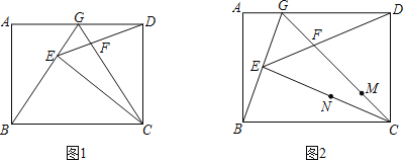
（1）如图1，若点G为AD的中点，则线段BG与CG有何数量关系？请说理由．
（2）如图2，若点E恰好为BG的中点，且AB=3，AG=k（0＜k＜3），求
的值（用含k的代数式表示）；
（3）在（2）有条件下，若M、N分别为GC、EC上的任意两点，连接NF、NM，当k=
时，求NF+NM的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
