
【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C
的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)当t为几秒时,BP平分∠ABC
(3)问t为何值时,△BCP为等腰三角形?
【答案】(1)16+2![]() ;(2)3;(3)6s或13s或12s或 10.8s.
;(2)3;(3)6s或13s或12s或 10.8s.
【解析】分析:(1)利用勾股定理得出AC=8cm,进而表示出AP的长,由勾股定理求出PB,进而得出答案;(2)过点P作PD⊥AB于点D,由HL证明Rt△BPD≌Rt△BPC,得出BD=BC=6cm,因此BD=10-6=4cm,设PC=x cm,则PA=(8-x)cm,由勾股定理得出方程,解方程即可;(3)利用分类讨论的思想和等腰三角形的特点及三角形的面积求出答案.
本题解析:
(1)∵∠C=90,AB=10cm,BC=6cm,∴有勾股定理得AC=8cm,动点P从点C开始,按![]() 的路径运动,且速度为每秒1cm
的路径运动,且速度为每秒1cm
∴出发2秒后,则CP=2cm,那么AP=6cm.
∵∠C=90°,
∴由勾股定理得PB=2![]() cm
cm
∴△ABP的周长为:AP+PB+AB=6+10+2![]() =(16+2
=(16+2![]() )cm;
)cm;
(2)如图2所示,过点P作PD⊥AB于点D,

∵BP平分∠ABC,∴PD=PC.
在Rt△BPD与Rt△BPC中, ![]() ,
,
∴Rt△BPD≌Rt△BPC(HL),
∴BD=BC=6 cm,
∴AD=106=4 cm.
设PC=x cm,则PA=(8x)cm
在Rt△APD中,PD+AD=PA,
即x+4=(8x),
解得:x=3,
∴当t=3秒时,AP平分∠CAB;
(3)若P在边AC上时,BC=CP=6cm,
此时用的时间为6s,△BCP为等腰三角形;
若P在AB边上时,有两种情况:
①若使BP=CB=6cm,此时AP=4cm,P运动的路程为12cm,
所以用的时间为12s,故t=12s时△BCP为等腰三角形;
②若CP=BC=6cm,过C作斜边AB的高,根据面积法求得高为4.8cm,
根据勾股定理求得BP=7.2cm,
所以P运动的路程为187.2=10.8cm,
∴t的时间为10.8s,△BCP为等腰三角形;
③若BP=CP时,则∠PCB=∠PBC,
∵∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,∴∠ACP=∠CAP,∴PA=PC
∴PA=PB=5cm
∴P的路程为13cm,所以时间为13s时,△BCP为等腰三角形。
∴t=6s或13s或12s或 10.8s 时△BCP为等腰三角形。


科目:初中数学 来源: 题型:
【题目】(2016湖南省岳阳市第24题)如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是__.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省邵阳市第24题)为了解市民对全市创卫工作的满意程度,某中学教学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
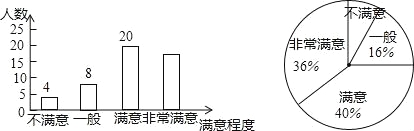
请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2为进行回访,已知4为市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com