练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知等腰△ABC的一长为6，另两边是一元二次方程x2-8x+12=0两个根，则等腰△ABC的周长是14．

    分析 解方程得出三角形的另外两边，根据周长公式可得．

    解答 解：解方程x2-8x+12=0得x1=2，x2=6，
    ∴等腰△ABC的周长为6+2+6=14，
    故答案为：14．

    点评 本题主要考查解方程或方程的根与系数的关系，熟练掌握解方程的能力和韦达定理是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．已知点C、D是线段AB的黄金分割点，AB=10，求线段AC与CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

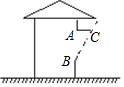    20．如图，某地夏季中午，当太阳移至房顶上方偏南时，光线与地面成80°角，房屋朝南的窗子高AB=1.8m，要在窗子外面上方安装水平挡光板AC，使午间光线不能直接射入室内，那么挡光板的宽度AC为（　　）
    A．1.8tan80°mB．1.8cos80°mC．$\frac{1.8}{sin80°}$ mD．$\frac{1.8}{tan80°}$ m

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．三角形的外心是这个三角形的（　　）
    A．三条中线的交点B．三条角平分线的交点
    C．三边的中垂线的交点D．三条高的交点

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，∠MON=90°，已知△ABC中，AC=BC=13，AB=10，△ABC的顶点A、B分别在边OM、ON上，当点B在边ON上运动时，A随之在OM上运动，△ABC的形状始终保持不变，在运动的过程中，点C到点O的最小距离为（　　）
    A．5B．7C．12D．$\sqrt{26}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．绍兴是著名的桥乡．如图，圆拱桥的桥顶到水面的距离CD为8m，桥拱半径OC为5m，则水面宽AB为（　　）
    A．4mB．5mC．6mD．8m

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，△ABC中，AD是高，CE是中线，点G是CE的中点，DG⊥CE，点G为垂足．
    （1）说明：DC=BE；
    （2）若∠AEC=72°，求∠BCE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．a=4，b=16，c=8，若a、c、b、d成比例线段．则d=32．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．你能找出规律吗？
    （1）计算：$\sqrt{4}$×$\sqrt{9}$=6，$\sqrt{4×9}$=6．$\sqrt{16}$×$\sqrt{25}$=20，$\sqrt{16×25}$=20．
    （2）请按找到的规律计算：①$\sqrt{5}$×$\sqrt{20}$；         ②$\sqrt{1\frac{2}{3}}$×$\sqrt{9\frac{3}{5}}$．

    查看答案和解析>>

    同步练习册答案