
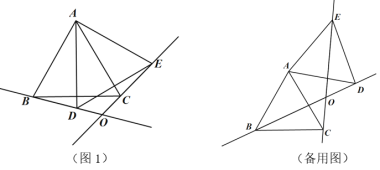
”¾ĢāÄæ”æŅŃÖŖ”÷ABCŹĒ±ß³¤ĪŖ6µÄµČ±ßČż½ĒŠĪ£®½«”÷ABCČʵćAÄꏱÕėŠż×Ŗ½Ē¦Č£Ø0”ć![]() ¦Č
¦Č![]() 180”ć£©µĆµ½”÷ADE£¬BDŗĶECĖłŌŚÖ±ĻßĻą½»ÓŚµćO£®
180”ć£©µĆµ½”÷ADE£¬BDŗĶECĖłŌŚÖ±ĻßĻą½»ÓŚµćO£®
£Ø1£©ČēĶ¼1£¬µ±0”ć![]() ¦Č
¦Č![]() 60”揱£¬”ĻBOCµÄ¶ČŹżŹĒ·ń±ä»Æ£æČō²»±ä£¬Ēó³ö”ĻBOCµÄ¶ČŹż£»Čō±ä»Æ£¬Ö±½ÓŠ“³ö”ĻBOCµÄ¶ČŹżµÄ±ä»Æ·¶Ī§£»
60”揱£¬”ĻBOCµÄ¶ČŹżŹĒ·ń±ä»Æ£æČō²»±ä£¬Ēó³ö”ĻBOCµÄ¶ČŹż£»Čō±ä»Æ£¬Ö±½ÓŠ“³ö”ĻBOCµÄ¶ČŹżµÄ±ä»Æ·¶Ī§£»
£Ø2£©ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±”÷BDEŹĒÖ±½ĒČż½ĒŠĪŹ±£¬ĒóBDµÄ³¤£»
£Ø3£©ŌŚ¦Č“Ó60”ćµ½120”ćµÄŠż×Ŗ¹ż³ĢÖŠ£¬Ö±½ÓŠ“³öµćOŌĖ¶ÆµÄĀ·¾¶³¤£®
”¾“š°ø”æ£Ø1£©²»±ä£¬![]() £Ø2£©
£Ø2£©![]() £»£Ø3£©
£»£Ø3£©![]()
”¾½āĪö”æ
£Ø1£©ĻČÖ¤Ć÷”÷ABD”Õ”÷ACE£¬Č»ŗóøł¾Ż½ĒµÄ“ś»»æÉµĆ³ö”ĻBOC=120”ć£»
£Ø2£©ĻČĶĘ³ö”ĻBDA=30”ć£¬øł¾ŻAB=AD=6£¬µĆ³ö”ĻABD=30”ć£¬×÷AM”ĶBDÓŚM£¬ŌŚ”÷ABMÖŠ£¬”ĻABM=30”ć£¬AB=6£¬”ĻBMA=90”ć£¬¼“æÉµĆ³ö“š£»
£Ø3£©ČēĶ¼£¬AD½»AEÓŚJ£®Éč”÷ABCµÄĶā½ÓŌ²µÄŌ²ŠÄĪŖK£®Ö¤Ć÷”ĻAOC£½120”ć£¬ĶĘ³öµćOµÄŌĖ¶Æ¹ģ¼£ŹĒKĪŖŌ²ŠÄ£¬KC°ė¾¶µÄŌ²»”£¬Ō²ŠÄ½ĒĪŖ60”ć£¬¼“æÉµĆ³ö“š°ø£®
½ā£ŗ£Ø1£©”ßAD=AE£¬AB=AC£¬”ĻBAD+”ĻDAC=”ĻDAC+”ĻCAE=60”ć£¬
”ą”ĻBAD=”ĻCAE£¬
”ą”÷ABD”Õ”÷ACE£¬
”ą”ĻAEC=”ĻADB£¬
”ß”ĻADO+”ĻADB=180”ć£¬
”ą”ĻADO+”ĻAEC=180”ć£¬
”ą”ĻDAE+”ĻBOC=180”ć£¬
”ß”ĻDAE=60”ć£¬
”ą”ĻBOC=120”ć£¬
”ą”ĻBOCµÄ¶ČŹż²»±ä£¬”ĻBOC=120”ć£»
£Ø2£©”ß”÷BDEŹĒÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻBDE=90”ć£¬
”ß”ĻBDA+”ĻADE=90”ć£¬”ĻADE=60”ć£¬
”ą”ĻBDA=30”ć£¬
”ßAB=AD=6£¬
”ą”ĻABD=30”ć£¬
×÷AM”ĶBDÓŚM£¬
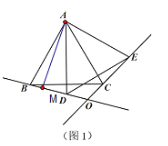
ŌŚ”÷ABMÖŠ£¬”ĻABM=30”ć£¬AB=6£¬”ĻBMA=90”ć£¬
”ąBM=![]() £¬
£¬
”ąBD=6![]() £»
£»
£Ø3£©ČēĶ¼ÖŠ£¬AD½»AEÓŚJ£®Éč”÷ABCµÄĶā½ÓŌ²µÄŌ²ŠÄĪŖK£¬
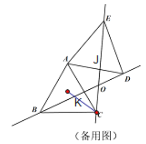
”ß”÷ABD”Õ”÷ACE£¬
”ą”ĻODJ£½”ĻAEJ£¬
”ß”ĻAJE£½”ĻOJD£¬
”ą”ĻEAJ£½”ĻJOD£½60”ć£¬
”ą”ĻAOC£½120”ć£¬
”ąµćOµÄŌĖ¶Æ¹ģ¼£ŹĒKĪŖŌ²ŠÄ£¬KC°ė¾¶µÄŌ²»”£¬Ō²ŠÄ½ĒĪŖ60”ć£¬
”ąµ±¦Č“Ó60”ćµ½120”ćµÄŠż×Ŗ¹ż³ĢÖŠ£¬KC=![]() ”¤
”¤![]() =
=![]() £¬
£¬
![]() =
=![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
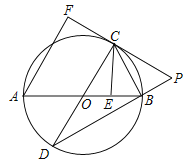
”¾ĢāÄæ”æ£Ø2017¹ć¶«Ź”£©ČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬AB=![]() £¬µćEĪŖĻ߶ĪOBÉĻŅ»µć£Ø²»ÓėO£¬BÖŲŗĻ£©£¬×÷CE”ĶOB£¬½»”ŃOÓŚµćC£¬“¹×ćĪŖµćE£¬×÷Ö±¾¶CD£¬¹żµćCµÄĒŠĻß½»DBµÄŃÓ³¤ĻßÓŚµćP£¬AF”ĶPCÓŚµćF£¬Į¬½ÓCB£®
£¬µćEĪŖĻ߶ĪOBÉĻŅ»µć£Ø²»ÓėO£¬BÖŲŗĻ£©£¬×÷CE”ĶOB£¬½»”ŃOÓŚµćC£¬“¹×ćĪŖµćE£¬×÷Ö±¾¶CD£¬¹żµćCµÄĒŠĻß½»DBµÄŃÓ³¤ĻßÓŚµćP£¬AF”ĶPCÓŚµćF£¬Į¬½ÓCB£®
£Ø1£©ĒóÖ¤£ŗCBŹĒ”ĻECPµÄĘ½·ÖĻߣ»
£Ø2£©ĒóÖ¤£ŗCF=CE£»
£Ø3£©µ±![]() Ź±£¬ĒóĮÓ»”
Ź±£¬ĒóĮÓ»”![]() µÄ³¤¶Č£Ø½į¹ū±£Įō¦Š£©
µÄ³¤¶Č£Ø½į¹ū±£Įō¦Š£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ½āѧɜÕĘĪÕĄ¬»ų·ÖĄąÖŖŹ¶µÄĒéæö£¬ŌöĒæѧɜ»·±£ŅāŹ¶£¬Ä³Ń§Š£¾ŁŠŠĮĖ”°Ą¬»ų·ÖĄąČĖČĖÓŠŌš”±µÄÖŖŹ¶²āŹŌ»ī¶Æ£¬ĻÖ“ÓøĆŠ£Ęß”¢°ĖÄź¼¶ÖŠø÷Ė껜³éČ”20ĆūѧɜµÄ²āŹŌ³É¼Ø£ØĀś·Ö10·Ö£¬6·Ö¼°6·ÖŅŌÉĻĪŖŗĻøń£©½ųŠŠÕūĄķ”¢ĆčŹöŗĶ·ÖĪö£¬ĻĀĆęøų³öĮĖ²æ·ÖŠÅĻ¢£®
ĘßÄź¼¶20ĆūѧɜµÄ²āŹŌ³É¼ØĪŖ£ŗ
7£¬8£¬7£¬9£¬7£¬6£¬5£¬9£¬10£¬9£¬8£¬5£¬8£¬7£¬6£¬7£¬9£¬7£¬10£¬6£®
Ęß”¢°ĖÄź¼¶³éČ”µÄѧɜµÄ²āŹŌ³É¼ØµÄĘ½¾łŹż”¢ÖŚŹż”¢ÖŠĪ»Źż”¢8·Ö¼°ŅŌÉĻČĖŹżĖłÕ¼°Ł·Ö±ČČēĻĀ±ķĖłŹ¾£ŗ
Äź¼¶ | Ę½¾łŹż | ÖŚŹż | ÖŠĪ»Źż | 8·Ö¼°ŅŌÉĻČĖŹżĖłÕ¼°Ł·Ö±Č |
ĘßÄź¼¶ | 7.5 | a | 7 | 45% |
°ĖÄź¼¶ | 7.5 | 8 | b | c |
°ĖÄź¼¶20ĆūѧɜµÄ²āŹŌ³É¼ØĢõŠĪĶ³¼ĘĶ¼ČēĶ¼£ŗ
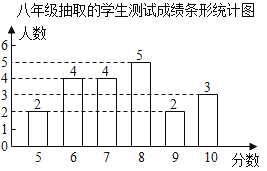
øł¾ŻŅŌÉĻŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ö±½ÓŠ“³öÉĻŹö±ķÖŠµÄa£¬b£¬cµÄÖµ£»
£Ø2£©øł¾ŻŅŌÉĻŹż¾Ż£¬ÄćČĻĪŖøĆŠ£Ęß”¢°ĖÄź¼¶ÖŠÄÄøöÄź¼¶Ń§ÉśÕĘĪÕĄ¬»ų·ÖĄąÖŖŹ¶½ĻŗĆ£æĒėĖµĆ÷ĄķÓɣ؊“³öŅ»ĢõĄķÓɼ“æÉ£©£»
£Ø3£©øĆŠ£Ęß”¢°ĖÄź¼¶¹²1200Ćūѧɜ²Ī¼ÓĮĖ“Ė“Ī²āŹŌ»ī¶Æ£¬¹Ą¼Ę²Ī¼Ó“Ė“Ī²āŹŌ»ī¶Æ³É¼ØŗĻøńµÄѧɜČĖŹżŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
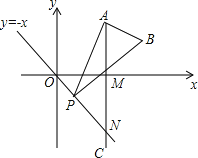
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµćAŹĒµŚŅ»ĻóĻŽÄŚŗį×ų±źĪŖ![]() µÄŅ»øö¶Øµć£¬AC”ĶxÖįÓŚµćM£¬½»Ö±Ļßy£½©xÓŚµćN£®ČōµćPŹĒĻ߶ĪONÉĻµÄŅ»øö¶Æµć£¬”ĻAPB£½30”ć£¬BA”ĶPA£¬ŌņµćPŌŚĻ߶ĪONÉĻŌĖ¶ÆŹ±£¬Aµć²»±ä£¬BµćĖęÖ®ŌĖ¶Æ£®Ēóµ±µćP“ÓµćOŌĖ¶Æµ½µćNŹ±£¬µćBŌĖ¶ÆµÄĀ·¾¶³¤ŹĒ_____£®
µÄŅ»øö¶Øµć£¬AC”ĶxÖįÓŚµćM£¬½»Ö±Ļßy£½©xÓŚµćN£®ČōµćPŹĒĻ߶ĪONÉĻµÄŅ»øö¶Æµć£¬”ĻAPB£½30”ć£¬BA”ĶPA£¬ŌņµćPŌŚĻ߶ĪONÉĻŌĖ¶ÆŹ±£¬Aµć²»±ä£¬BµćĖęÖ®ŌĖ¶Æ£®Ēóµ±µćP“ÓµćOŌĖ¶Æµ½µćNŹ±£¬µćBŌĖ¶ÆµÄĀ·¾¶³¤ŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖŌöĒæ»·¾³±£»¤ŅāŹ¶£¬ŌŚ”°ŹĄ½ē»·¾³ČÕ”±µ±Ģģ£¬ŌŚ»·±£¾Ö¹¤×÷ČĖŌ±Öøµ¼ĻĀ£¬ČōøÉĆū”°»·±£Š”ĪĄŹæ”±×é³ÉµÄ”°æŲÖĘŌėÉłĪŪČ¾”±æĪĢāѧĻ°ŃŠ¾æŠ”×飬Ė껜³é²éĮĖČ«ŹŠ40øöŌėÉł²āĮæµćŌŚÄ³Ź±æĢµÄŌėɳɳ¼¶£Øµ„Ī»£ŗdB£©£¬²¢½«³é²éµĆµ½µÄŹż¾Ż½ųŠŠÕūĄķ£ØÉčĖł²āŹż¾ŻŹĒÕżÕūŹż£©£¬µĆʵŹż·Ö²¼±ķČēĻĀ£ŗ
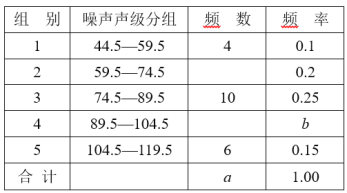

øł¾Ż±ķÖŠĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĘµŹż·Ö²¼±ķÖŠµÄa£½ £¬b£½ £»
£Ø2£©²¹³äĶźÕūʵŹż·Ö²¼Ö±·½Ķ¼£»
£Ø3£©Õā×鏿¾ŻµÄÖŠĪ»ŹżĀäŌŚµŚ Š”×éÄŚ£»
£Ø4£©Čē¹ūČ«ŹŠ¹²ÓŠ400øö²āĮæµć£¬ÄĒĆ“ŌŚÕāŅ»Ź±æĢŌėɳɳ¼¶Š”ÓŚ75dBµÄ²āĮæµćŌ¼ÓŠ¶ąÉŁøö£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ2018Äź9ŌĀ21ČÕ”°ŃĪ³Ē“óĶĀķ”°Ė³Ąū»Ų¹é£¬ČēĶ¼£¬Š”ĄöŗĶŠ”Ć÷¾ö¶ØÓĆĖłŃ§µÄÖŖŹ¶²āĮæ“óĶĀķABµÄøß¶Č£¬°“ÕÕŅŌĻĀ·½Ź½ŗĻ×÷²¢¼ĒĀ¼ĖłµĆŹż¾Ż£ŗŠ”Ć÷²āµĆ»ł×łĻĀ²æBE³¤ĪŖ1.8Ć×£¬»ł×łBCøßĪŖ6.12Ć×£¬ŌŚEµć“¦²āµĆµćFµÄŃö½ĒĪŖ80.72”ć£¬Š”ĄöŃŲÖ±ĻßBE²½ŠŠµ½“ļµćD“¦²āµĆµćAŗĶµćFµÄŃö½Ē·Ö±šĪŖ60.18”ćŗĶ50.75”ć£¬ČōA”¢B”¢C”¢D”¢E”¢FŌŚĶ¬Ņ»Ę½ĆęÄŚĒŅB”¢E”¢DŗĶA”¢C”¢B·Ö±šŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬Ēė·Ö±šĒó³öCFŗĶ“óĶĀķABµÄøß¶Č£®£Ø½į¹ū¾«Č·µ½0.01Ć×£¬²Īæ¼Źż¾Żsin80.72”ć£½0.987£¬cos80.72”ć£½0.161£¬tan80.72”ć£½6.12£¬sin60.18”ć£½0.868£¬cos60.18”ć£½0.497£¬tan60.18”ć£½1.74£¬sin50.75”ć£½0.774£¬cos50.75”ć£½0.663£¬tan50.75”ć£½1.224£©
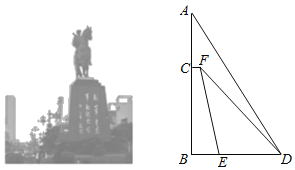
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖ¼ĶÄī”°ĪåĖÄŌĖ¶Æ”±100ÖÜÄź£¬Ä³Š£¾ŁŠŠĮĖÕ÷ĪıČČü£¬øĆŠ£Ń§ÉśČ«²æ²Ī¼ÓĮĖ±ČČü£®±ČČüÉčÖĆŅ»µČ”¢¶žµČ”¢ČżµČČżøö½±Ļī£¬ČüŗóøĆŠ£¶Ōѧɜ»ń½±Ēéæö×öĮĖ³éŃłµ÷²é£¬²¢½«ĖłµĆŹż¾Ż»ęÖĘ³ÉČēĶ¼ĖłŹ¾µÄĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£®øł¾ŻĶ¼ÖŠŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
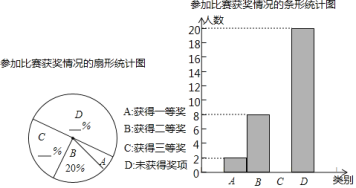
£Ø1£©±¾“Ī³éŃłµ÷²éѧɜµÄČĖŹżĪŖ”” ””£®
£Ø2£©²¹Č«Į½øöĶ³¼ĘĶ¼£¬²¢Ēó³öÉČŠĪĶ³¼ĘĶ¼ÖŠAĖł¶ŌÓ¦ÉČŠĪŌ²ŠÄ½ĒµÄ¶ČŹż£®
£Ø3£©ČōøĆŠ£¹²ÓŠ840Ćūѧɜ£¬Ēėøł¾Ż³éŃłµ÷²é½į¹ū¹Ą¼Ę»ńµĆČżµČ½±µÄČĖŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æAŹŠ×¼±øÕł““Č«¹śĪĄÉś³ĒŹŠ£®Ä³Š”Ēų»ż¼«ĻģÓ¦£¬¾ö¶ØŌŚŠ”ĒųÄŚ°²×°Ą¬»ų·ÖĄąµÄĢįŹ¾ÅĘŗĶĄ¬»ųĻ䣬Čō¹ŗĀņ2øöĢįŹ¾ÅĘŗĶ3øöĄ¬»ųĻä¹²Šč550ŌŖ£¬ĒŅĄ¬»ųĻäµÄµ„¼ŪŹĒĢįŹ¾Åʵ„¼ŪµÄ3±¶£®
£Ø1£©ĒóĢįŹ¾ÅĘŗĶĄ¬»ųĻäµÄµ„¼Ūø÷ŹĒ¶ąÉŁŌŖ?
£Ø2£©øĆŠ”ĒųÖĮÉŁŠčŅŖ°²·Å48øöĄ¬»ųĻ䣬Čē¹ū¹ŗĀņĢįŹ¾ÅĘŗĶĄ¬»ųĻä¹²100øö£¬ĒŅ·ŃÓĆ²»³¬¹ż10000ŌŖ£¬ĒėÄćĮŠ¾Ł³öĖłÓŠ¹ŗĀņ·½°ø£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÖŠ¹śŹĒ×īŌē·¢ĻÖ²¢ĄūÓĆ²čµÄ¹ś¼Ņ£¬ŠĪ³ÉĮĖ¾ßÓŠ¶ĄĢŲ÷ČĮ¦µÄ²čĪÄ»Æ2020Äź5ŌĀ21ČÕŅŌ”°²čŗĶŹĄ½ē¹²Ę·¹²Ļķ”±ĪŖÖ÷ĢāµÄµŚŅ»½ģ¹ś¼Ź²čČÕŌŚÖŠ¹śÕŁæŖ£®Ä³²čµźÓĆ4000ŌŖ¹ŗ½ųĮĖAÖÖ²čŅ¶ČōøÉŗŠ£¬ÓĆ8400ŌŖ¹ŗ½ųBÖÖ²čŅ¶ČōøÉŗŠ£¬Ėł¹ŗBÖÖ²čŅ¶±ČAÖÖ²čŅ¶¶ą10ŗŠ£¬ĒŅBÖÖ²čŅ¶ĆæŗŠ½ų¼ŪŹĒAÖÖ²čŅ¶ĆæŗŠ½ų¼ŪµÄ1.4±¶£®
£Ø1£©A£¬BĮ½ÖÖ²čŅ¶ĆæŗŠ½ų¼Ū·Ö±šĪŖ¶ąÉŁŌŖ£æ
£Ø2£©µŚŅ»“ĪĖł¹ŗ²čŅ¶Č«²æŹŪĶźŗ󵌶ž“Ī¹ŗ½ųA£¬BĮ½ÖÖ²čŅ¶¹²100ŗŠ£Ø½ų¼Ū²»±ä£©£¬AÖÖ²čŅ¶µÄŹŪ¼ŪŹĒĆæŗŠ300ŌŖ£¬BÖÖ²čŅ¶µÄŹŪ¼ŪŹĒĆæŗŠ400ŌŖ£®Į½ÖÖ²čŅ¶ø÷ŹŪ³öŅ»°ėŗó£¬ĪŖĒģ×£¹ś¼Ź²čČÕ£¬Į½ÖÖ²čŅ¶¾ł“ņĘßÕŪĻśŹŪ£¬Č«²æŹŪ³öŗ󣬵Ś¶ž“ĪĖł¹ŗ²čŅ¶µÄĄūČóĪŖ5800ŌŖ£Ø²»æ¼ĀĒĘäĖūŅņĖŲ£©£¬Ē󱾓Ī¹ŗ½ųA£¬BĮ½ÖÖ²čŅ¶ø÷¶ąÉŁŗŠ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com