
分析 根据比较有理数的大小的方法:(1)负数<0<正数;(2)两个负数,绝对值大的反而小,即可解答.
解答 解:∵|-$\frac{4}{7}$|=$\frac{4}{7}=\frac{12}{21}$,|-$\frac{2}{3}$|=$\frac{2}{3}$=$\frac{14}{21}$,$\frac{12}{21}<\frac{14}{21}$,
∴-$\frac{4}{7}$>-$\frac{2}{3}$;
∵-(-7)=7,-|-7|=-7,7>-7,
∴-(-7)>-|-7|,
故答案为:>,>.
点评 本题考查了有理数的大小比较,解决本题的关键是熟记比较有理数的大小的方法:(1)负数<0<正数;(2)两个负数,绝对值大的反而小.


科目:初中数学 来源: 题型:解答题
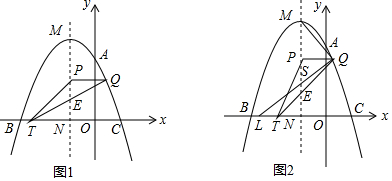
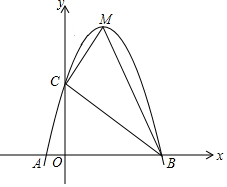 已知:如图,二次函数y=ax2+bx+3的图象与x轴交于A、B两点,其中A点坐标为(-1,0),且抛物线经过点(2,3),M为抛物线的顶点.
已知:如图,二次函数y=ax2+bx+3的图象与x轴交于A、B两点,其中A点坐标为(-1,0),且抛物线经过点(2,3),M为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
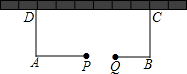 如图,某养鸡专业户准备利用一面墙(墙的长度大于50米),用长50米的篱笆围成一个鸡的活动场地矩形ABCD,其中AB边上有一个宽2米的门(即PQ=2米)且门不需用篱笆.请你帮助设计一下,当矩形的长AB是多少米时,此矩形面积最大?最大面积是多少平方米?
如图,某养鸡专业户准备利用一面墙(墙的长度大于50米),用长50米的篱笆围成一个鸡的活动场地矩形ABCD,其中AB边上有一个宽2米的门(即PQ=2米)且门不需用篱笆.请你帮助设计一下,当矩形的长AB是多少米时,此矩形面积最大?最大面积是多少平方米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
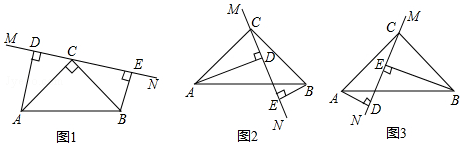
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
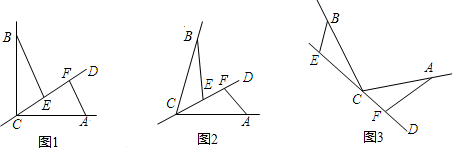
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com