
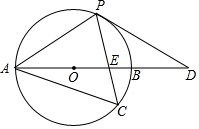
 如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.分析 (1)连结OP,根据圆周角定理可得∠AOP=2∠ACP=120°,然后计算出∠PAD和∠D的度数,进而可得∠OPD=90°,从而证明PD是⊙O的切线;
(2)连结BC,首先求出∠CAB=∠ABC=∠APC=45°,然后可得AC长,再证明△CAE∽△CPA,进而可得$\frac{CA}{CP}=\frac{CE}{CA}$,然后可得CE•CP的值.
解答 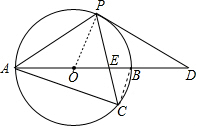 解:(1)如图,PD是⊙O的切线.
解:(1)如图,PD是⊙O的切线.
证明如下:
连结OP,
∵∠ACP=60°,
∴∠AOP=120°,
∵OA=OP,
∴∠OAP=∠OPA=30°,
∵PA=PD,
∴∠PAO=∠D=30°,
∴∠OPD=90°,
∴PD是⊙O的切线.
(2)连结BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵C为弧AB的中点,
∴∠CAB=∠ABC=∠APC=45°,
∵AB=4,$AC=ABsin{45°}=2\sqrt{2}$.
∵∠C=∠C,∠CAB=∠APC,
∴△CAE∽△CPA,
∴$\frac{CA}{CP}=\frac{CE}{CA}$,
∴CP•CE=CA2=(2$\sqrt{2}$)2=8.
点评 此题主要考查了切线的判定和相似三角形的性质和判定,关键是掌握切线的判定定理和相似三角形的判定与性质定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.076×108 | B. | 2076×106 | C. | 0.2076×108 | D. | 2.076×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
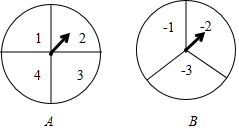 爸爸下班回家呆了一张同事送的《加勒比海盗5》的电影票,结果两小儿子都想要去看,于是爸爸提议用如图所示的两个转盘(其中转盘A被等分成4个扇形,且4个扇形内依次标有数字:1,2,3,4;转盘B被等分成3个扇形,且3个扇形内依次标有数字:-1,-2,-3)做游戏来决定谁去.
爸爸下班回家呆了一张同事送的《加勒比海盗5》的电影票,结果两小儿子都想要去看,于是爸爸提议用如图所示的两个转盘(其中转盘A被等分成4个扇形,且4个扇形内依次标有数字:1,2,3,4;转盘B被等分成3个扇形,且3个扇形内依次标有数字:-1,-2,-3)做游戏来决定谁去.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
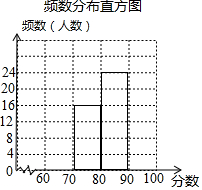 九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.| 分数段 | 频数(人数) |
| 60≤x<70 | a |
| 70≤x<80 | 16 |
| 80≤x<90 | 24 |
| 90≤x<100 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
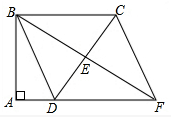 如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com