

���� ��1����A��B���������������ߵĽ���ʽ�����ɵó�a��bֵ���ٽ������߽���ʽ��ɶ���ʽ�����ɵó��������ꣻ
��2���������������ε����ʣ���m��ʾ��FD�ij��ȣ����ɵ㵽ֱ�ߵľ��빫ʽ����m��ʾ����E��ֱ��AD�ľ��룬�������ε������ʽ���ܱ�ɳ���DEF��������䷽���ɵõ���ֵ���������ȡ��ֵʱ��m��ֵ���ҳ�E�����꣬�ٸ��ݵ㵽ֱ�ߵľ��빫ʽ�����������ʱ��E��BD�ľ��룻
��3�������������ε�����֮�ʹ��ڵ����ߣ������ҵ�ʹ��MA+MC��ֵ��Сʱ�ĵ�M��λ�ã�����ֱ�ߵĽ��㼴�ɵó�M�����ꣻ�����������ε�����֮��С�ڵ����ߣ������ҵ�ʹحNA-NCح��ֵ���ʱ��N��λ�ã�����ֱ�ߵĽ��㼴�ɵó�N�����꣮
��� �⣺��1����������y=ax2+bx-2��a��0������A��-1��0����B��4��0����
����$\left\{\begin{array}{l}{a-b-2=0}\\{16a+4b-2=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{3}{2}}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{2}$x2-$\frac{3}{2}$x-2��
��y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2=$\frac{1}{2}$${��x-\frac{3}{2}��}^{2}$-$\frac{25}{8}$��
�ඥ��D������Ϊ��$\frac{3}{2}$��-$\frac{25}{8}$����
��2���������⣬����ͼ��1�����£�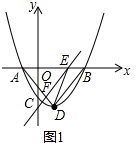
��AEAE�ij�Ϊm����E������Ϊ��m-1��0����
��A��-1��0����B��4��0����D��$\frac{3}{2}$��-$\frac{25}{8}$����
��AB=5��AD=BD=$\frac{5\sqrt{41}}{8}$��
��EF��BD��
���AFE=��ADB����AEF=��ABD��
���AEF�ס�ABD��
��$\frac{AF}{AD}$=$\frac{AE}{AB}$��AF=$\frac{\sqrt{41}}{8}$m��FD=AD-AF=$\frac{\sqrt{41}}{8}$��5-m����
��ֱ��AD�Ľ���ʽΪy=kx+b��
��A��-1��0����D��$\frac{3}{2}$��-$\frac{25}{8}$����ֱ��AD�ϣ�
����$\left\{\begin{array}{l}{0=-k+b}\\{-\frac{25}{8}=\frac{3}{2}k+b}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{5}{4}}\\{b=-\frac{5}{4}}\end{array}\right.$��
��ֱ��AD�Ľ���ʽΪy=-$\frac{5}{4}$x-$\frac{5}{4}$����$\frac{5}{4}$x+y+$\frac{5}{4}$=0��
��E��ֱ��AD�ľ���h=$\frac{|\frac{5}{4}��m-1��+\frac{5}{4}|}{\sqrt{��\frac{5}{4}��^{2}+{1}^{2}}}$=$\frac{5\sqrt{41}}{41}$m��
��DEF�����=$\frac{1}{2}$•FD•h=-$\frac{5}{16}$m2+$\frac{25}{16}$m=-$\frac{5}{16}$${��m-\frac{5}{2}��}^{2}$+$\frac{125}{64}$��
��m=$\frac{5}{2}$ʱ����DEF�����������ֵΪ$\frac{125}{64}$��
��ֱ��BD�Ľ���ʽΪy=k1x+b1��
����$\left\{\begin{array}{l}{0=4{k}_{1}+{b}_{1}}\\{\frac{25}{8}=\frac{3}{2}{k}_{1}+{b}_{1}}\end{array}\right.$�����$\left\{\begin{array}{l}{{k}_{1}=\frac{5}{4}}\\{{b}_{1}=-5}\end{array}\right.$��
��ֱ��BD�Ľ���ʽy=$\frac{5}{4}$x-5����$\frac{5}{4}$x-y-5=0��
�ߵ�E����Ϊ��$\frac{3}{2}$��0����
���E��BD�ľ���Ϊ$\frac{|\frac{5}{4}��\frac{3}{2}-5|}{\sqrt{��\frac{5}{4}��^{2}+{1}^{2}}}$=$\frac{25\sqrt{41}}{82}$��
��3��������BC���������߶Գ��ύBC�ڵ�M������MA����ͼ2��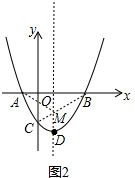
�������ߵĶԳ��Կ�֪��MA=MB��
MA+MC=MB+MC=BC��
�ߵ�M���ڶԳ������ƶ�ʱ������BC�ϣ�����MB+MC��BA������������֮�ʹ��ڵ����ߣ���
�൱��M��BC��ʱ��MA+MC=BC��С��
��x=0���������߽���ʽy=$\frac{1}{2}$x2-$\frac{3}{2}$x-2�У���y=-2��
����C������0��-2����
��ֱ��BC�Ľ���ʽΪy=k3x-2��
����B��4��0�����룬��0=4k3-2�����k3=$\frac{1}{2}$��
��ֱ��BC�Ľ���ʽΪy=$\frac{1}{2}$x-2��
�ɣ�1����֪�����ߵĶԳ���Ϊx=$\frac{3}{2}$��
��$\left\{\begin{array}{l}{y=\frac{1}{2}x-2}\\{x=\frac{3}{2}}\end{array}\right.$����$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=-\frac{5}{4}}\end{array}\right.$��
��ʹ��MA+MC��ֵ��С��M������Ϊ��$\frac{3}{2}$��-$\frac{5}{4}$����
������AC�����ӳ�AC�������߶Գ����ڵ�N����ͼ3��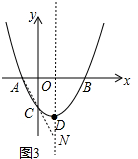
�ߵ�N���ڶԳ������ƶ�ʱ������ֱ��AC�ϣ�����|NA-NC|��AC������������֮��С�ڵ����ߣ���
�൱��N��ֱ��AC��ʱ��|NA-NC|=AC���
�ߵ�C��0��-2����
����ֱ��AC�Ľ���ʽΪy=k4x-2��
����A��-1��0�����룬��0=-k4-2�����k4=-2��
��ֱ��AC�Ľ���ʽΪy=-2x-2��
�����ߵĶԳ���Ϊx=$\frac{3}{2}$��
��$\left\{\begin{array}{l}{y=-2x-2}\\{x=\frac{3}{2}}\end{array}\right.$����$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=-5}\end{array}\right.$��
��ʹحNA-NCح��ֵ����N������Ϊ��$\frac{3}{2}$��-5����
���� ���⿼���˶��κ������ۺ����ã�����Ĺؼ�����1�������������룬���Ԫһ�η��̼��ɣ���2���������������Ƶ������Լ��㵽ֱ�ߵľ��룬�����ú�m�Ĵ���ʽ��ʾ����������⼫ֵ���⼴�ɣ���3���μ������ε����߹�ϵ������֮�ʹ��ڵ����ߣ�����֮��С�ڵ����ߣ�


 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪E��F�ֱ�Ϊƽ���ı���ABCD�ĶԱ�AD��BC�ϵĵ㣬��DE=BF��EM��AC��M��FN��AC��N��EF��AC�ڵ�O����֤��
��ͼ����֪E��F�ֱ�Ϊƽ���ı���ABCD�ĶԱ�AD��BC�ϵĵ㣬��DE=BF��EM��AC��M��FN��AC��N��EF��AC�ڵ�O����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
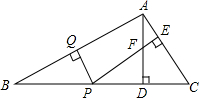 ��ͼ����ABC�У���B=22.5�㣬AB�Ĵ�ֱƽ���߽�AB�ڵ�Q����BC�ڵ�P��PE��AC�ڵ�E��AD��BC�ڵ�D��AD��PE�ڵ�F����֤��DF=DC��
��ͼ����ABC�У���B=22.5�㣬AB�Ĵ�ֱƽ���߽�AB�ڵ�Q����BC�ڵ�P��PE��AC�ڵ�E��AD��BC�ڵ�D��AD��PE�ڵ�F����֤��DF=DC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |
| B�� |
| ||||||||||||||||||||||
| C�� |
| D�� |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����CAB����CDE���ǵ���ֱ�������Σ�M��DB�е㣬��֤��CM��AE��
��ͼ����CAB����CDE���ǵ���ֱ�������Σ�M��DB�е㣬��֤��CM��AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������y=ax2+2��a+1��x+$\frac{3}{2}$��a��0����x�ύ��A��x1��0����B��x2��0����x1��x2�����㣬��y�ύ��C�㣮�������������еĶ���D��
��֪������y=ax2+2��a+1��x+$\frac{3}{2}$��a��0����x�ύ��A��x1��0����B��x2��0����x1��x2�����㣬��y�ύ��C�㣮�������������еĶ���D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com