
【题目】如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确的有:___________
①AD=EC;②BM=BN;③MN∥AC;④EM=MB.

【答案】①②③
【解析】∵△ABE,△BCD均为等边三角形,
∴AB=BE,BC=BD,∠ABE=∠CBD=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC中
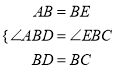
∴△ABD≌△EBC(SAS),
∴AD=EC,故①正确;
∴∠DAB=∠BEC,
又由上可知∠ABE=∠CBD=60°,
∴∠EBD=60°,
在△ABM和△EBN中
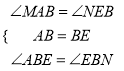
∴△ABM≌△EBN(ASA),
∴BM=BN,故②正确;
∴△BMN为等边三角形,
∴∠NMB=∠ABM=60°,
∴MN∥AC,故③正确;
若EM=MB,则AM平分∠EAB,
则∠DAB=30°,而由条件无法得出这一条件,
故④不正确;
综上可知正确的有①②③,
故答案为:①②③.


科目:初中数学 来源: 题型:
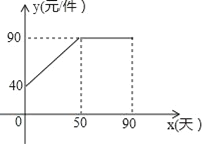
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.连接直线外一点与直线上各点的所有线段中,垂线段最短
B.互补的角是邻补角
C.两条直线被第三条直线所截,同旁内角互补
D.过一点有且只有一条直线与已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题.
(1)先化简,再求值: ![]() ÷
÷![]() ,其中x=
,其中x=![]() +1.
+1.
(2)分解因式:8(x2-2y2)-x(7x+y)+xy.
(3)解不等式![]() ≤
≤![]() -1,并把解集表示在数轴上.
-1,并把解集表示在数轴上.
![]()
(4)解不等式组![]() 并将解集在数轴上表示出来.
并将解集在数轴上表示出来.
![]()
(5)解方程: ![]() +
+![]() =4.
=4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )

A. 36 B. 12 C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com