
【题目】在△ABC与△A′B′C′中,有下列条件:(1) ![]() ,(2)
,(2) ![]() ;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组
B.2组
C.3组
D.4组
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE. 
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD2OE;
(3)若cos∠BAD= ![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小米是一个爱动脑筋的孩子,他用如下方法作∠AOB的角平分线: 作法:如图,
⑴在射线OA上任取一点C,过点C作CD∥OB;
⑵以点C为圆心,CO的长为半径作弧,交CD于点E;
⑶作射线OE.
所以射线OE就是∠AOB的角平分线.请回答:小米的作图依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用10000元购进甲、乙两种商品,销售完成后共获利2200元,其中甲种商品每件进价60元,售价70元;乙种商品每件进价50元,售价65元.
(1)求该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,且购进甲、乙商品的数量分别与第一次相同,甲种商品按原售价出售,而乙种商品降价销售,要使第二次购进的两种商品全部售出后,获利不少于1800元,乙种商品最多可以降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,过点(x1 , 0),﹣3<x1<﹣2,对称轴为直线x=﹣1.给出四个结论:①abc>0;②2a+b=0;③b2>4ac;④3b+2c>0,其中正确的结论有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,BC=6cm.射线 AG∥BC,点 E 从点 A 出发沿射线 AG 以 2cm/s 的速度运动,当点 E 先出发 1s 后,点 F 也从点 B 出发沿射线 BC 以![]() cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
(1)当 t 为何值时,∠BAF<∠BAC;
(2)当 t 为何值时,AE=CF;
(3)当 t 为何值时,S△ABF+S△ACE<S△ABC.
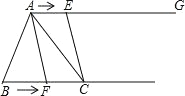
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的顶点为D(﹣1,2),其部分图象如图所示,给出下列四个结论: ①a<0; ②b2﹣4ac>0;③2a﹣b=0;④若点P(x0 , y0)在抛物线上,则ax02+bx0+c≤a﹣b+c.其中结论正确的是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com