
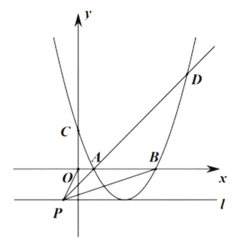
【题目】如图所示,二次函数![]() 的图像(记为抛物线
的图像(记为抛物线![]() )与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为
)与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,
,![]() ,且过点
,且过点![]() ,求该二次函数的表达式;
,求该二次函数的表达式;
(2)若关于x的一元二次方程![]() 的判别式
的判别式![]() .求证:当
.求证:当![]() 时,二次函数
时,二次函数![]() 的图像与x轴没有交点.
的图像与x轴没有交点.
(3)若![]() ,点P的坐标为
,点P的坐标为![]() ,过点P作直线l垂直于y轴,且抛物线的
,过点P作直线l垂直于y轴,且抛物线的![]() 顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线
顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线![]() 交于点D,若
交于点D,若![]() ,求
,求![]() 的最小值.
的最小值.
科目:初中数学 来源: 题型:
【题目】已知点![]() 在
在![]() 上.则下列命题为真命题的是( )
上.则下列命题为真命题的是( )
A.若半径![]() 平分弦
平分弦![]() .则四边形
.则四边形![]() 是平行四边形
是平行四边形
B.若四边形![]() 是平行四边形.则
是平行四边形.则![]()
C.若![]() .则弦
.则弦![]() 平分半径
平分半径![]()
D.若弦![]() 平分半径
平分半径![]() .则半径
.则半径![]() 平分弦
平分弦![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与直线y=mx交于点A(2,2).
(x>0)的图象与直线y=mx交于点A(2,2).
(1)求k,m的值;
(2)点P的横坐标为n(n>0),且在直线y=mx上,过点P作平行于x轴的直线,交y轴于点M,交函数y=![]() (x>0)的图象于点N.
(x>0)的图象于点N.
①n=1时,用等式表示线段PM与PN的数量关系,并说明理由;
②若PN≥3PM,结合函数的图象,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
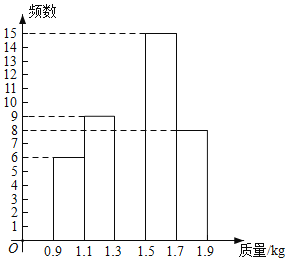
【题目】2020年是脱贫攻坚年,为实现全员脱贫目标,某村贫困户在当地政府支持帮助下,办起了养鸡场,经过一段时间精心饲养,总量为3000只的一批鸡可以出售.现从中随机抽取50只,得到它们质量的统计数据如下:
质量 | 组中值 | 数量(只) |
| 1.0 | 6 |
| 1.2 | 9 |
| 1.4 | a |
| 1.6 | 15 |
| 1.8 | 8 |
根据以上信息,解答下列问题:
(1)表中![]() ______,补全频数分布直方图;
______,补全频数分布直方图;
(2)这批鸡中质量不小于![]() 的大约有多少只?
的大约有多少只?
(3)这些贫因户的总收入达到54000元,就能实现全员脱贫目标.按15元![]() 的价格售出这批鸡后,该村贫困户能否脱贫?
的价格售出这批鸡后,该村贫困户能否脱贫?
查看答案和解析>>
科目:初中数学 来源: 题型:
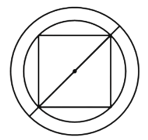
【题目】据《汉书律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也”斛是中国古代的一种量器,“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为:正方形的外接一个圆,此圆外是一个同心圆”,如图所示.
问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为________尺.(结果用最简根式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
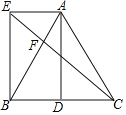
【题目】如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
●操作发现:
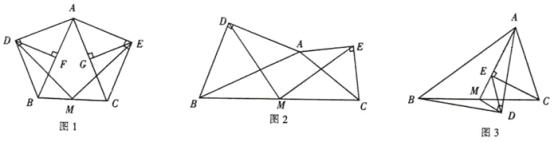
在等腰△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论正确的是 (填序号即可)
①AF=AG=![]() AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.
AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.
●数学思考:
在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD和ME具有怎样的数量和位置关系?请给出证明过程;
●类比探索:
在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,试判断△MED的形状.
答: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陕西省某甜瓜基地因“规模大、品质好、品牌亮”吸引了周边大批水果批发商订购,该基地对需要送货上门且购买量在![]() (含1000kg和3000kg)的客户制定了两种销售方案(客户只能选择其中一种方案),已知该基地甜瓜批发价随市场变化波动,设某天批发价为每千克m元.
(含1000kg和3000kg)的客户制定了两种销售方案(客户只能选择其中一种方案),已知该基地甜瓜批发价随市场变化波动,设某天批发价为每千克m元.
方案一:每千克![]() 元,免运费;
元,免运费;
方案二:每千克m元,客户需支付运费1200元.
(1)请分别写出这一天按方案一、方案二购买这种甜瓜的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)当购买量x在什么范围时,选择方案二比方案一付款少;
(3)已知5月某天批发价为每千克8元,某水果批发商计划用25000元在这一天购买尽可能多的这种甜瓜并需要送货上门,那么他在这两种方案中,应选择哪一种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,OA平分
,OA平分![]() 交BC于点O,以O为圆心,OC长为半径作圆交BC于点D.
交BC于点O,以O为圆心,OC长为半径作圆交BC于点D.

(1)如图1,求证:AB为![]() 的切线;
的切线;
(2)如图2,AB与![]() 相切于点E,连接CE交OA于点F.
相切于点E,连接CE交OA于点F.
①试判断线段OA与CE的关系,并说明理由.
②若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com