
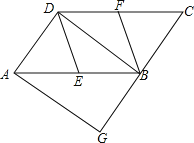
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据已知条件证明BE=DF,BE∥DF,从而得出四边形DFBE是平行四边形,即可证明DE∥BF,
(2)先证明DE=BE,再根据邻边相等的平行四边形是菱形,从而得出结论.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE=![]() AB,DF=
AB,DF=![]() CD.
CD.
∴BE=DF,BE∥DF,
∴四边形DFBE是平行四边形,
∴DE∥BF;
(2)∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
在Rt△ADB中
∵E为AB的中点,
∴AE=BE=DE,
∵四边形DFBE是平行四边形,
∴四边形DEBF是菱形.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
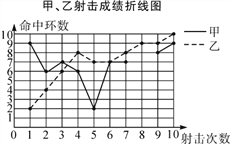
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | |||
乙 | 1 |
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
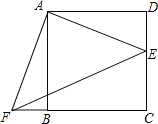
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△AOB中,将扇形COD按图1摆放,使扇形的半径OC、OD分别与OA、OB重合,OA=OB=2,OC=OD=1,固定等边△AOB不动,让扇形COD绕点O逆时针旋转,线段AC、BD也随之变化,设旋转角为α.(0<α≤360°) 
(1)当OC∥AB时,旋转角α=度;
(2)线段AC与BD有何数量关系,请仅就图2给出证明. 
(3)当A、C、D三点共线时,求BD的长.
(4)P是线段AB上任意一点,在扇形COD的旋转过程中,请直接写出线段PC的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在日历中任意圈出一个3×3的正方形,则里面九个数不满足的关系式是( )

A. a1+a2+a3+a7+a8+a9=2(a4+a5+a6)
B. a1+a4+a7+a3+a6+a9=2(a2+a5+a8)
C. a1+a2+a3+a4+a5+a6+a7+a8+a9=9a5
D. (a3+a6+a9)﹣(a1+a4+a7)=(a2+a5+a8)
查看答案和解析>>
科目:初中数学 来源: 题型:
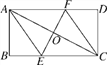
【题目】如图,将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,连接AE,CF,AC.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,①求菱形AECF的边长;②求折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班体育委员统计了全班45名同学一周的体育锻炼时间(单位:小时),并绘制了如图所示的折线统计图,下列说法中错误的是( )

A. 锻炼时间是9小时的人数最多 B. 锻炼时间是10小时的有10人
C. 锻炼时间是11小时的有4人 D. 锻炼时间不低于9小时的有14人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com