
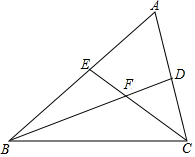
 如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,
如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,分析 (1)根据三角形的内角和等于180°列式求出∠ABC+∠ACB,再根据角平分线的定义求出∠FBC+∠FCB,然后利用三角形的内角和等于180°列式计算即可得解.
(2)在BC上取一点O使得BO=BE,易证∠BFE=∠CFD=60°,即可证明△BFE≌△BFO,可得∠BFO=∠BFE=60°,即可证明△OCF≌△DCF,可得CO=CD,根据BC=BO+OC即可证明.
解答 解:(1)在△ABC中,∠ABC+∠ACB=180°-∠A=180°-60°=120°,
∵∠ABC,∠ACB的平分线BE,CD相交于点F,
∴∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,
∴∠FBC+∠FCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×120°=60°,
在△BCF中,∠BFC=180°-(∠FBC+∠FCB)=180°-60°=120°.
(2)证明:在BC上取一点O,使得BO=BE,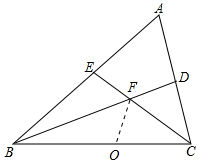
∵∠A=60°,BD、CE是△ABC的角平分线,
∴∠BFC=120°,
∴∠BFE=∠CFD=60°,
在△BFE和△BFO中,
$\left\{\begin{array}{l}{BF=BF}\\{∠FBE=∠FBO}\\{BE=BO}\end{array}\right.$,
∴△BFE≌△BFO,(SAS)
∴∠BFO=∠BFE=60°,
∴∠CFO=∠BFC-∠BFO=60°,
在△OCF和△OCD中,
$\left\{\begin{array}{l}{∠CFO=∠CFD=60°}\\{CF=CF}\\{∠FCO=∠FCD}\end{array}\right.$,
∴△OCF≌△DCF(ASA),
∴CO=CD,
∵BC=BO+CO,
∴BC=BE+CD.
点评 本题考查了全等三角形的判定和性质性质、三角形的内角和定理,角平分线的定义,解题的关键是学会添加辅助线构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{33}{1296}$ | B. | $\frac{334}{1296}$ | C. | $\frac{343}{1296}$ | D. | $\frac{433}{1296}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
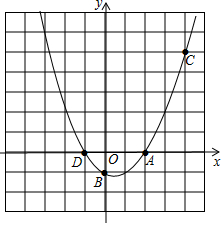 如图,已知二次函数y=ax2+bx+c经过点A(2,0),B(0,-1),C(4,5)三点.
如图,已知二次函数y=ax2+bx+c经过点A(2,0),B(0,-1),C(4,5)三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
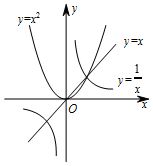 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象| A. | 正确的命题是①④ | B. | 错误的命题是②③④ | C. | 正确的命题是①② | D. | 错误的命题只有③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛物线开口向下 | B. | 抛物线经过点(3,4) | ||
| C. | 抛物线的对称轴是直线x=1 | D. | 抛物线与x轴有两个交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |-2|与2 | B. | -2与-$\frac{1}{2}$ | C. | -2与$\root{3}{-8}$ | D. | -2与$\sqrt{(-2)^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com