
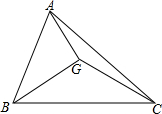
 已知G是△ABC的重心,AG=1,BG=3,CG=2$\sqrt{2}$,求S△ABC.
已知G是△ABC的重心,AG=1,BG=3,CG=2$\sqrt{2}$,求S△ABC. 分析 延长AG到GE,与BC相交于D,使DG=DE,则△BDG≌△CDE,所以CE=BG=6,根据重心的性质可求得DG=DE=3,则GE=6,又CG=10,所以△CGE是直角三角形,并可求得其面积,从而得出△BGC的面积,即可求得△ABC的面积.
解答 解: 延长AG到E,与BC相交于D,使DG=DE,则△BDG≌△CDE,
延长AG到E,与BC相交于D,使DG=DE,则△BDG≌△CDE,
∴CE=BG=3,
∵DG=$\frac{1}{2}$AG=$\frac{1}{2}$,
∴DG=DE=$\frac{1}{2}$,
∴GE=1,
∵CG=2$\sqrt{2}$,
∴△CGE是直角三角形,
∴S△GBC=S△CGE=$\frac{1}{2}$×3×2$\sqrt{2}$=3$\sqrt{2}$,
∴S△ABC=3S△GBC=3$\sqrt{3}$.
点评 本题考查了重心的概念和性质,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com