练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．已知：如图，D是△ABC的边BC上的一点，且AB=BD=AD=DC，求∠B，∠C，∠BAC，∠DAC的度数．

    分析 易得△ABD是等边三角形，那么∠B=∠ADB=∠BAD=60°，由AD=CD可得∠C=∠CAD，因为∠ADB=∠C+∠CAD，那么∠C=∠CAD=30°，再根据∠BAC=∠BAD+∠CAD即可求得∠BAC的度数．

    解答 解：∵AB=BD=AD，
    ∴△ABD是等边三角形，
    ∴∠B=∠ADB=∠BAD=60°，
    ∵AD=CD，
    ∴∠C=∠CAD，
    ∵∠ADB=∠C+∠CAD，
    ∴∠C=∠CAD=30°，
    ∴∠BAC=∠BAD+∠CAD=90°．

    点评 此题考查了等腰三角形的性质，用到的知识点为：等边三角形的每个内角都是60°；等边对等角；三角形的一个外角等于和它不相邻的两个内角的和．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．已知$\sqrt{a-b}$+b2-4b+4=0，求ab的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．方程2（x-1）2=5的解为x1=1+$\frac{\sqrt{10}}{2}$，x2=1-$\frac{\sqrt{10}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．二次函数y=ax2+bx+c有最大值为5，若关于x的方程|ax2+bx+c|=t最多有三个不相等的实数根，其中t为常数t≠0，则t的取值范围是（　　）
    A．t≥5B．t＞5C．t＜5D．t≤5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．因式分解：m2+4n-mn-4m=（m-n）（m-4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．设△ABC是正三角形，点P在△ABC外，且与点A在直线BC异侧，∠BPC=120°，求证：PA=PB+PC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．为了求1+2+22+23+24+…+22008的值，可令S=1+2+22+23+24+…+22008，然后扩大两倍变成：2S=2+22+23+24+…+22008+22009，再让两式相减，因此有2S-S=22009-1，所以：S=22009-1，即1+2+22+23+24+…+22008=22009-1．
    仿照上面的计算过程计算下列式子：
    （1）计算1+5+52+53+54+…+52011的值．
    （2）计算1+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{10}}$的值．
    （3）计算1+a+a2+a3+a4+…+an的值（a≠1）．（用字母表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列计算正确的是（　　）
    A．（-2ab2）3=-2a3b6B．b3•b3=b6C．a3÷a=2aD．（a5）2=a7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

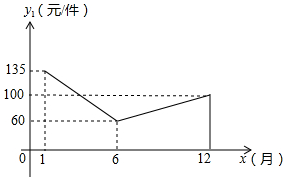    3．某商场在1月至12月份经销某种品牌的服装，由于受到时令的影响，该种服装的销售情况如下：销售价格y1（元/件）与销售月份x（月）的关系大致满足如图的函数，销售成本y2（元/件）与销售月份x（月）满足y2=$\left\{\begin{array}{l}{-10x+100（1≤x＜6，且x为整数）}\\{\frac{14}{3}x（6≤x≤12，且x为整数）}\end{array}\right.$，月销售量y3（件）与销售月份x（月）满足y3=-10x+20．
    （1）根据图象求出销售价格y1（元/件）与销售月份x（月）之间的函数关系式；（6≤x≤12且x为整数）；
    （2）求出该服装月销售利润W（元）与月份x（月）之间的函数关系式，并求出哪个月份的销售利润最大？最大利润是多少？（6≤x≤12且x为整数）..

    查看答案和解析>>

    同步练习册答案