练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】对于反比例函数，下列说法中不正确的是（ ）

    A. 图像经过点（1.-2）

    B. 图像分布在第二第四象限

    C. x>0时，y随x增大而增大

    D. 若点A（）B（）在图像上，若,则

    【答案】D

    【解析】

    根据反比例函数图象上点的坐标特征及反比例函数的性质，即函数所在的象限和增减性对各选项作出判断．

    A.把点（1，-2）代入得：-2=-2，故该选项正确，不符合题意，

    B.∵k=-2<0，

    ∴函数图像分布在第二第四象限，故该选项正确，不符合题意，

    C.∵k=-2<0，

    ∴x>0时，y随x增大而增大，故该选项正确，不符合题意，

    D.∵反比例函数的图象在二、四象限，

    ∴x<0时，y>0，x>0时，y<0，

    ∴x1<0<x2时，y1>y2，故该选项错误，符合题意，

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中,O为坐标原点,抛物线交x轴于点A(l,0)、B(3,0),交y轴于点C.

    (1)如图1,求抛物线的解析式；

    (2)如图2,点P为对称轴右侧第四象限抛物线上一点,连接PA并延长交y轴于点K,点P横坐标为t,△PCK的面积为S,求S与t的函数关系式(直接写出自变量t的取值范围）；

    (3)如图3,在(2)的条件下,过点A作AD⊥AP交y轴于点D.连接OP,过点O作OE⊥OP交AD延长线于点E,当OE=OP时,延长EA交抛物线于点Q,点M在直线EC上,连接QM,交AB于点H，将射线QM绕点Q逆时针旋转45°,得到射线QN交AB于点F,交直线EC于点N,若AH:HF=3:5,求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（如图1所示）在△ABC中，∠ACB=90°，∠A=30°，BC=4，沿斜边AB的中线CD把这个三角形剪成△AC1D1和△BC2D2两个三角形（如图2所示）．将△AC1D1沿直线D2B方向平移（点A，D1，D2，B始终在同一直线上），当点D1于点B重合时，平移停止．设平移距离D1D2为x，△AC1D1和△BC2D2的重叠部分面积为y，在y与x的函数图象大致是（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为acm的正方形内，截去两个以正方形的边长acm为直径的半圆.(以下结果保π)

    (1)图中阴影部分的周长为______cm，

    (2)图中阴影部分的面积为________cm2；

    (3)当a＝2时，求图中阴影部分的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于80元，经市场调查，每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：

    售价x（元/千克）

    50

    60

    70

    销售量y（千克）

    100

    80

    60

    （1）求y与x之间的函数表达式；

    （2）设商品每天的总利润为W（元），则当售价x定为多少元时，厂商每天能获得最大利润？最大利润是多少？

    （3）如果超市要获得每天不低于1350元的利润，且符合超市自己的规定，那么该商品每千克售价的取值范围是多少？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设0!表示自然数由1到n的连乘积，并规定0!＝1，Anm＝，nm＝（n≥0，n≥m）例如1!＝1，2!＝1×2＝2，3!＝1×2×3＝6，A53＝＝60，C64＝＝15，请回答以下问题：

    （1）求C32，A32；

    （2）试根据C32，A32，2!的值写出C32，A32，2!满足的等量关系；试根据C43，A43，3!的值写出C43，A43，3!满足的等量关系；试根据C54，A54，4!的值写出C54，A54，4!满足的等量关系；

    （3）探究Amn，Cmn与n!之间满足的等量关系（不需要证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

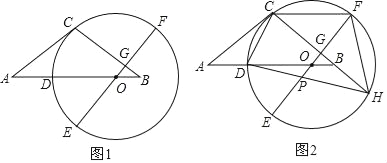
    【题目】如图1，等腰△ABC中，AC=BC，点O在AB边上，以O为圆心的圆经过点C，交AB边于点D，EF为⊙O的直径，EF⊥BC于点G，且D是的中点．

    （1）求证：AC是⊙O的切线；

    （2）如图2，延长CB交⊙O于点H，连接HD交OE于点P，连接CF，求证：CF=DO+OP；

    （3）在（2）的条件下，连接CD，若tan∠HDC=，CG=4，求OP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB＝4，动点P从A出发，在直线AB上以每秒3个单位的速度向右运动，到达B后立即返回，回到A后停止运动，动点Q与P同时从A出发，在直线AB上以每秒1个单位的速度向左运动，当P停止运动时，点Q也停止运动，设点P的运动时间为t秒．

    （1）若t＝1，则BP的长是　 　PQ的长是　 　．

    （2）当点P回到点A时，求BQ的长．

    （3）在直线AB上取点C，使B是线段PC的中点，在点P的整个运动过程中，是否存在AC＝AQ+3，若存在，求出此时t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=kx+b的图象与x轴交于点A，与反比例函数y=（x＞0）的图象交于点B（2，n），过点B作BC⊥x轴于点C，点P（3n﹣4，1）是该反比例函数图象上的一点，且∠PBC=∠ABC，求反比例函数和一次函数的表达式．

    查看答案和解析>>

    同步练习册答案