

分析 (1)先根据已知条件得到∠ADE=∠OFD,再根据∠A=∠A,即可判定△ADE∽△AFD,进而得到 $\frac{AD}{AF}$=$\frac{AE}{AD}$,即AD2=AE•AF;
(2)①取EG的中点H,连接CH、DH、CD,根据Rt△EDG、Rt△ECG,点H为EG的中点,即可得到CH=EH=GH=DH=$\frac{1}{2}$EG,进而得出点C、E、D、G在以点H为圆心,EG为直径的圆上,故EG>CD,再根据Rt△ABC,DB=AD,可得CD=DB=AD=$\frac{1}{2}$AB,据此可得EG>BD;
②将△ADE绕着点D旋转180°,得到△BDP,连接GP,由(1)中AD2=AE•AF,可得16=AE•(AE+6),解得AE=2;再根据DG垂直平分EP,得出GE=GP=y,然后过点P作PQ⊥BG于Q,在Rt△BPQ中,根据∠GBP=60°,BP=2,即可得出BQ=1,PQ=$\sqrt{3}$,GQ=BG-BQ=x-1;最后在Rt△GPQ中,根据 PG2=GQ2+PQ2,即可得出y2=(x-1)2+($\sqrt{3}$)2,进而得到y=$\sqrt{{x}^{2}-2x+4}$.
解答 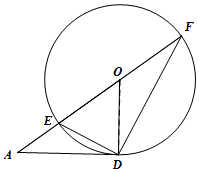 解:(1)如图,∵AD是⊙O的切线,
解:(1)如图,∵AD是⊙O的切线,
∴OD⊥AD,即∠ADE+∠EDO=90°,
∵EF是直径,
∴∠EDF=90°,即∠EDO+∠ODF=90°,
∴∠ADE=∠ODF,
∵OD=OF,
∴∠ODF=∠OFD,
∴∠ADE=∠OFD,
又∵∠A=∠A,
∴△ADE∽△AFD,
∴$\frac{AD}{AF}$=$\frac{AE}{AD}$,即AD2=AE•AF;
(2)①当α=90°时,EG>BD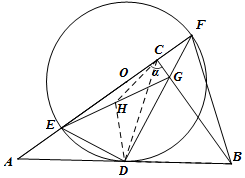 .
.
理由:如图,取EG的中点H,连接CH、DH、CD,
∵Rt△EDG、Rt△ECG,点H为EG的中点,
∴CH=EH=GH=DH=$\frac{1}{2}$EG,
∴点C、E、D、G在以点H为圆心,EG为直径的圆上,
∴EG>CD,
∵Rt△ABC,DB=AD,
∴CD=DB=AD=$\frac{1}{2}$AB,
∴EG>BD;
②当α=120°时,如图,将△ADE绕着点D旋转180°,得到△BDP,连接GP,
由(1)中AD2=AE•AF,得16=AE•(AE+6),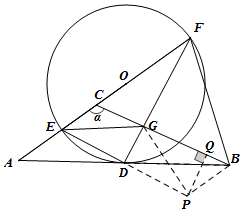
解得AE=2,或AE=-8(舍去),
∵△ADE≌△BDP,
∴ED=DP,AE=BP=2,∠A=∠DBP,
∵∠EDF=90°,
∴DG垂直平分EP,
∴GE=GP=y,
∵∠A+∠ABC=180°-120°=60°,
∴∠DBP+∠ABC=60°,
即∠GBP=60°,
如图,过点P作PQ⊥BG于Q,
在Rt△BPQ中,∠GBP=60°,BP=2,
∴BQ=1,PQ=$\sqrt{3}$,
∴GQ=BG-BQ=x-1,
在Rt△GPQ中,PQ=$\sqrt{3}$,GQ=x-1,GP=y,
∴PG2=GQ2+PQ2,
即y2=(x-1)2+($\sqrt{3}$)2,
∴y=$\sqrt{{x}^{2}-2x+4}$.
点评 本题属于圆的综合题,主要考查了相似三角形的判定与性质,圆周角定理,直角三角形斜边上中线的性质,全等三角形的性质,含30°角的直角三角形的性质以及勾股定理的综合应用,解决问题的关键是作辅助线构造全等三角形和直角三角形,依据全等三角形的性质以及勾股定理列出表达式进行变形.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件OA=OC,使四边形ABCD是菱形.(只需添加一个即可)
如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件OA=OC,使四边形ABCD是菱形.(只需添加一个即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
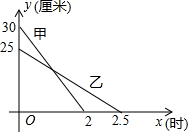 在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时所剩余部分的高度y(cm)与燃烧时间x(h)的关系如图所示,请根据图象提供的信息解答下列问题:
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时所剩余部分的高度y(cm)与燃烧时间x(h)的关系如图所示,请根据图象提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com