
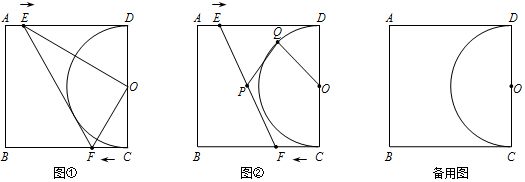
·ÖĪö £Ø1£©¢ŁČēĶ¼£¬ÉčEFÓė°ėŌ²ĻąĒŠÓŚµćG£¬ÓÉĒŠĻß³¤¶ØĄķæÉÖŖED=EG£¬FC=FG£¬ŌŚRt”÷EHFÖŠ£¬ĄūÓĆ¹“¹É¶ØĄķĮŠ³ö·½³Ģ¼“æɽā¾öĪŹĢā£»
¢Ś·ÖČżÖÖĒéŠĪĢÖĀŪ£¬·Ö±šĮŠ³ö·½³ĢĒó½ā¼“æÉ£»
£Ø2£©¢Łµ±µćPŌŚ°ėŌ²ÉĻŹ±£¬PQµÄ×īŠ”ÖµĪŖ0£¬“ĖŹ±PQ+OQµÄ×īŠ”ÖµĪŖ1£®¢Śµ±µćFŌĖ¶Æµ½BŹ±£¬µćPÓėµćOÖ®¼äµÄ½įĀŪ×ī“󣬵±QÓėDÖŲŗĻŹ±£¬PQ+OQµÄÖµ×ī“ó£»
½ā“š ½ā£ŗ£Ø1£©¢ŁČēĶ¼£¬ÉčEFÓė°ėŌ²ĻąĒŠÓŚµćG£¬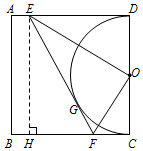
¹żµćE×÷EH”ĶBC£¬“¹×ćĪŖµćH£®ČēĶ¼¢Ł£¬
”ßĖıߊĪABCDŹĒÕż·½ŠĪ£¬
”ąAB=BC=CD=AD=2£¬”ĻA=”ĻB=”ĻADC=”ĻBCD=90”ć£¬
”ąOD”ĶAD£¬
”ąADÓė°ėŌ²ĻąĒŠÓŚµćD£¬
Ķ¬ĄķæÉÖ¤£ŗBCÓė°ėŌ²ĻąĒŠÓŚµćC£¬
”ąED=EG=2-t£¬CF=FG=2t£¬
”ąEF=2+t£¬
”ßEH”ĶBC£¬“¹×ćĪŖµćH£¬”ą”ĻBHE=90”ć£¬
”ß”ĻA=”ĻB=90”ć£¬”ąĖıߊĪABHEŹĒ¾ŲŠĪ£¬
”ąEH=AB=2£¬BH=AE=t£¬
”ąHF=2-3t£¬
ŌŚ”÷EHFÖŠ£¬”ĻEHF=90”ć£¬
”ąEH2+HF2=EF2£¬
”ą22+£Ø2-3t£©2=£Ø2+t£©2£¬
½āÕāøö·½³Ģ£¬µĆt1=1-$\frac{\sqrt{2}}{2}$£¼1£¬t2=1+$\frac{\sqrt{2}}{2}$£¾1£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬
”ąµ±EFÓė°ėŌ²ĻąĒŠŹ±£¬tµÄÖµĪŖ1-$\frac{\sqrt{2}}{2}$£®
¢ŚŌŚ”÷EDOÖŠ£¬”ß”ĻEDO=90”ć£¬
”ąOE2=t2-4t+5£¬
Ķ¬ĄķæÉÖ¤£ŗOF2=1+4t2£¬EF2=9t2-12t+8£¬
µŚŅ»ÖÖĒéæö£ŗµ±OE=OFŹ±£¬ŌņOE2=OF2£¬
”ąt2-4t+5=1+4t2£¬
½āÕāøö·½³Ģ£¬µĆt1=$\frac{2}{3}$£¼1£¬t2=-2£¼0£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬
µŚ¶žÖÖĒéæö£ŗµ±OE=EFŹ±£¬ŌņOE2=EF2£¬
”ąt2-4t+5=9t2-12t+8£¬“Ė·½³ĢĪŽ½ā£¬
µŚČżÖÖĒéæö£ŗµ±OF=EFŹ±£¬ŌņOF2=EF2£¬
”ą1+4t2=9t2-12t+8£¬
½āÕāøö·½³Ģ£¬µĆt1=1£¬t2=1.4£¾1£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬
×ŪÉĻĖłŹö£ŗµ±”÷EOFŹĒµČŃüČż½ĒŠĪŹ±£¬tµÄÖµĪŖ$\frac{2}{3}$»ņ1£®
£Ø2£©ČēĶ¼
¢Łµ±µćPŌŚ°ėŌ²ÉĻŹ±£¬PQµÄ×īŠ”ÖµĪŖ0£¬“ĖŹ±PQ+OQµÄ×īŠ”ÖµĪŖ1£®
¢Śµ±µćFŌĖ¶Æµ½BŹ±£¬µćPÓėµćOÖ®¼äµÄ½įĀŪ×ī“󣬵±QÓėDÖŲŗĻŹ±£¬PQ+OQµÄÖµ×ī“ó£¬×ī“óÖµ=$\sqrt{{1}^{2}+£Ø\frac{3}{2}£©^{2}}$+1=1+$\frac{\sqrt{13}}{2}$£®
”ąPQ+OQµÄ×īŠ”ÖµĪŖ1£¬×ī“óÖµĪŖ1+$\frac{\sqrt{13}}{2}$£®
µćĘĄ ±¾Ģāæ¼²éŌ²×ŪŗĻĢā”¢ĒŠĻß³¤¶ØĄķ”¢¹“¹É¶ØĄķ”¢Õż·½ŠĪµÄŠŌÖŹ”¢µČŃüČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĮé»īŌĖÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£¬Ń§»į¹¹½Ø·½³Ģ½ā¾öĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬”÷ABCÖŠ£¬AB=BC£¬ŅŌABĪŖÖ±¾¶µÄ”ŃO½»ACÓŚµćD£¬ĒŅCD=BD£®
ČēĶ¼£¬”÷ABCÖŠ£¬AB=BC£¬ŅŌABĪŖÖ±¾¶µÄ”ŃO½»ACÓŚµćD£¬ĒŅCD=BD£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
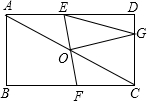 ČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬¶Ō½ĒĻßACµÄÖŠµćĪŖO£¬¹żO×÷Ö±ĻßEF½»ADÓŚE£¬½»BCÓŚF£®
ČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬¶Ō½ĒĻßACµÄÖŠµćĪŖO£¬¹żO×÷Ö±ĻßEF½»ADÓŚE£¬½»BCÓŚF£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | a+1£¾b+1 | B£® | a-1£¼b-1 | C£® | ac£¼bc | D£® | $\frac{a}{3}$£¾$\frac{b}{3}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
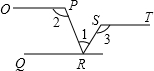 ČēĶ¼£¬ŅŃÖŖOP”ĪQR”ĪST£¬ŌņĻĀĮŠµČŹ½ÖŠÕżČ·µÄŹĒ£Ø””””£©
ČēĶ¼£¬ŅŃÖŖOP”ĪQR”ĪST£¬ŌņĻĀĮŠµČŹ½ÖŠÕżČ·µÄŹĒ£Ø””””£©| A£® | ”Ļ1+”Ļ2-”Ļ3=90”ć | B£® | ”Ļ1-”Ļ2+”Ļ3=180”ć | C£® | ”Ļ2+”Ļ3-”Ļ1=180”ć | D£® | ”Ļ1+”Ļ2+”Ļ3=180”ć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
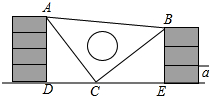 æĪ¼ä£¬Š”Ć÷ÄĆ×ÅĄĻŹ¦µÄµČŃüÖ±½ĒČż½Ē°åĶę£¬²»Š”ŠÄµōµ½Į½Ē½Ö®¼ä£¬ČēĶ¼ĖłŹ¾£®
æĪ¼ä£¬Š”Ć÷ÄĆ×ÅĄĻŹ¦µÄµČŃüÖ±½ĒČż½Ē°åĶę£¬²»Š”ŠÄµōµ½Į½Ē½Ö®¼ä£¬ČēĶ¼ĖłŹ¾£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com