
【题目】△ABC中,∠C=90°,AB=1,tanA=![]() ,过AB边上一点P作PE⊥AC于E,PF⊥BC于F,E、F是垂足,则EF的最小值等于_____.
,过AB边上一点P作PE⊥AC于E,PF⊥BC于F,E、F是垂足,则EF的最小值等于_____.
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AB与x轴、y轴分别交于点A、B,作等腰直角三角形ABC,使∠BAC=90°,将△ABC沿着射线AB平移得到△A′B′C′,当点A′与点B重合时停止运动.设平移距离为m,△A′B′C′与△ABO重合部分的面积为S,S关于m的函数图象如图2所示.(其中0≤m≤![]() 时,函数的解析式不同)
时,函数的解析式不同)
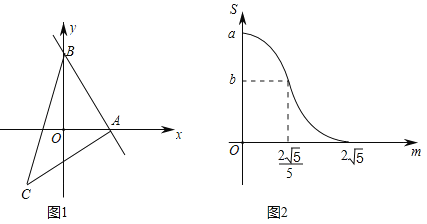
(1)填空:a= ;
(2)求直线AB的解析式;
(3)求S关于m的解析式,并写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD切⊙O于C点,弦CF⊥AB于E点,连结AC.
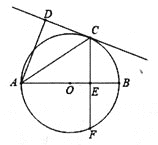
(1)求证:∠ACD=∠ACF;
(2)当AD⊥CD,BE=2cm,CF=8cm,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
在综合与实践课上,老师让同学们以“大小不等的两个正方形”为主题开展数学活动,如图1,现有一个边长为![]() 的正方形
的正方形![]() ,点
,点![]() 从对角线
从对角线![]() 的点
的点![]() 出发向点
出发向点![]() 运动,连接
运动,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,以
,以![]() 为边在
为边在![]() 右侧作正方形
右侧作正方形![]() ,边
,边![]() 与射线
与射线![]() 交于点
交于点![]() .
.
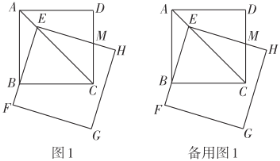
操作发现
(1)点![]() 在运动过程中,判断线段
在运动过程中,判断线段![]() 与线段
与线段![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
实践探究
(2)在点![]() 的运动过程中,某时刻正方形
的运动过程中,某时刻正方形![]() 与正方形
与正方形![]() 重叠的四边形
重叠的四边形![]() 的面积是
的面积是![]() ,求此时
,求此时![]() 的长;
的长;
探究拓广
(3)请借助备用图2,探究当点![]() 不与点
不与点![]() ,
,![]() 重合时,线段
重合时,线段![]() ,
,![]() 与
与![]() 之间存在的数量关系,请直接写出.
之间存在的数量关系,请直接写出.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图7,在四边形ABCD中,AB=BC,∠ABC=60°,E是CD边上一点,连接BE,以BE为一边作等边三角形BEF.请用直尺在图中连接一条线段,使图中存在经过旋转可完全重合的两个三角形,并说明这两个三角形经过什么样的旋转可重合.
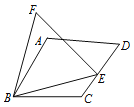
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com