
【题目】如图,□ABCD中,点E是AB边的中点,延长DE交CB的延长线于点F.
⑴ 求证:△ADE≌△BFE;
⑵ 若DE⊥AB且DE=AB,连接EC,求∠FEC的度数.
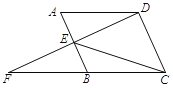
【答案】⑴ 见解析;⑵ ∠FEC=135°
【解析】
(1)由平行四边形的性质证得∠A=∠FBE,∠ADE=∠F,再由点E是AB中点,得AE=BE,即证得△ADE≌△BFE;
(2)由□ABCD得AB∥DC,AB=CD ,由DE⊥AB且DE=AB易证∠CDF=90°,可得∠DEC =45°,从而可得结论.
⑴ ∵ 四边形ABCD是平行四边形
∴ AD∥BC
∴ ∠A=∠ABF
∵ 点E是AB的中点
∴ AE=BE
在△ABE和△ACD中
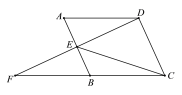
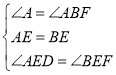
∴ △ADE≌△BFE
⑵ ∵ 四边形ABCD是平行四边形
∴ AB∥DC,AB=CD
∴ ∠CDF=∠BEF
∵ DE⊥AB
∴ ∠BEF=90°
∴ ∠CDF=90°
∵ DE=AB
∴ DE=DC
∴ ∠DEC=∠DCE=45°
∴ ∠FEC=135°


科目:初中数学 来源: 题型:
【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2垂足为A2,交x轴于点A3过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4,过点A4作A4A5⊥A3A4,垂足为A4…交x轴于点A5:过点A5作A5A6⊥A4A5,A5A6⊥A4A5垂足为A5,交y轴于点A6…按此规律进行下去,则点A2019的横坐标为_____.
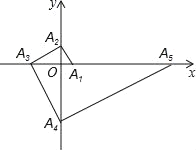
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是_____.
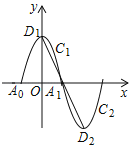
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() -1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
-1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
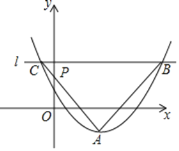
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角为直角的四边形叫做“对直角四边形”.如图1,四边形ABCD中,∠A=∠C=90°,则四边形ABCD是“对直角四边形”.

(1)“对角线相等的对直角四边形是矩形”是______命题;(填“真”或“假”)
(2)如图2,在对直角四边形ABCD中,∠DAB<90°,AD+CD=AB+BC.试说明△ADC的面积与△ABC的面积相等;
(3)如图3,在△ABC中,∠C=90°,AC=6,BC=8,过AB的中点D作射线DP∥AC,交BC于点O,∠BDP与∠ADP的角平分线分别交BC,AC于点E、F.
①图中是“对直角四边形”的是______;
②当OP的长是______时,四边形DEPF为对直角四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=![]() ,E是AD边上的一点(点E与点A和点D不重合),BE的垂直平分线交AB于点M,交DC于点N.
,E是AD边上的一点(点E与点A和点D不重合),BE的垂直平分线交AB于点M,交DC于点N.
(1)证明:MN = BE.
(2)设AE=![]() ,四边形ADNM的面积为S,写出S关于
,四边形ADNM的面积为S,写出S关于![]() 的函数关系式.
的函数关系式.
(3)当AE为何值时,四边形ADNM的面积最大?最大值是多少?
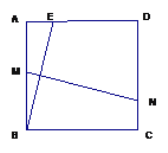
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=10°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1 P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2 P3;……

请按照上面的要求继续操作并探究:
∠P3 P2 P4=_____°;按照上面的要求一直画下去,得到点Pn,若之后就不能再画出符合要求点Pn+1了,则n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com