
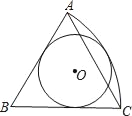
【题目】如图,在边长为2的等边三角形ABC中,以B为圆心,AB为半径作![]() ,在扇形BAC内作⊙O与AB、BC、
,在扇形BAC内作⊙O与AB、BC、![]() 都相切,则⊙O的周长等于( )
都相切,则⊙O的周长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D. π
D. π
【答案】C
【解析】
连接OB并延长与![]() 交于点E,设AB与圆的切点为D,连接OD,由三角形ABC为等边三角形得到BA=BC,且∠ABC=60°,再由以B为圆心,AB为半径作
交于点E,设AB与圆的切点为D,连接OD,由三角形ABC为等边三角形得到BA=BC,且∠ABC=60°,再由以B为圆心,AB为半径作![]() ,得到BE=BA=BC=2,根据对称性得到∠ABE=30°,由AB与圆O相切,利用切线的性质得到OD垂直于AB,在直角三角形BOD中,利用30°所对的直角边等于斜边的一半得到OD等于OB的一半,设OD=OE=x,可得出OB=2x,由BO+OE=BE=2,列出关于x的方程,求出方程的解得到x的值,即为圆O的半径,即可求出圆O的周长.
,得到BE=BA=BC=2,根据对称性得到∠ABE=30°,由AB与圆O相切,利用切线的性质得到OD垂直于AB,在直角三角形BOD中,利用30°所对的直角边等于斜边的一半得到OD等于OB的一半,设OD=OE=x,可得出OB=2x,由BO+OE=BE=2,列出关于x的方程,求出方程的解得到x的值,即为圆O的半径,即可求出圆O的周长.
解:连接OB并延长与![]() 交于点E,设AB与圆的切点为D,连接OD,
交于点E,设AB与圆的切点为D,连接OD,
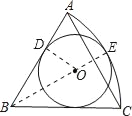
∵△ABC为等边三角形,以B为圆心,AB为半径作![]() ,
,
∴∠ABC=60°,BA=BC=BE=2,
由对称性得到:∠ABE=30°,
∵AB为⊙O的切线,
∴OD⊥AB,
在Rt△BOD中,∠ABE=30°,设OD=OE=x,
可得OB=2x,
∴OB+OE=BE,
即2x+x=2,
解得:x=![]() ,
,
即⊙O的半径为![]() ,
,
∴⊙O的周长为:![]() =
=![]() π.
π.
故选:C.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】2015年12月16日,南京大报恩寺遗址公园正式对外开放.某校数学兴趣小组想测量大报恩塔的高度.如图,成员小明利用测角仪在B处测得塔顶的仰角α=63.5°,然后沿着正对该塔的方向前进了13.1m到达E处,再次测得塔顶的仰角β=71.6°.测角仪BD的高度为1.4m,那么该塔AC的高度是多少?(参考数据:sin63.5°≈0.90,cos63.5°≈0.45,tan63.5°≈2.00,sin71.6°≈0.95,cos71.6°≈0.30,tan71.6°≈3.00)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市有一种“喜之郎“果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,轴截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,这个包装盒的长![]() 不计重合部分,两个果冻之间没有挤压
不计重合部分,两个果冻之间没有挤压![]() 至少为
至少为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实施产业精准扶贫,帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克,到了收获季节投入市场销售时,调查市场行情后,发现该蜜柚不会亏本,且每天的销售量y(千克)与销售单价x(元)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某村农户今年共采摘蜜柚12000千克,若该品种蜜柚的保质期为50天,按照(2)的销售方式,能否在保质期内全部销售完这批蜜柚?若能,请说明理由;若不能,应定销售价为多少元时,既能销售完又能获得最大利润?

查看答案和解析>>
科目:初中数学 来源: 题型:
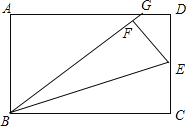
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
(1)小明发现DG⊥BE,请你帮他说明理由.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
(3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由.
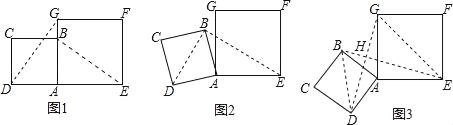
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡AB长60![]() 米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
(1)若修建的斜坡BE的坡比为![]() :1,求休闲平台DE的长是多少米?
:1,求休闲平台DE的长是多少米?
(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G,H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
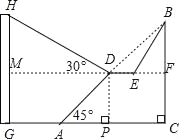
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE= ![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
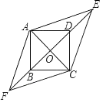
A. DE=1 B. tan∠AFO= ![]() C. AF=
C. AF= ![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com