
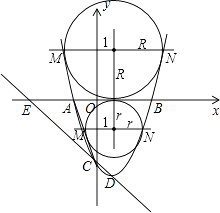
【题目】如图,在平面直角坐标系中,函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,OC=3OA.
(1)求这个二次函数的表达式;
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
【答案】
(1)
解:∵点B的坐标为(3,0),OB=OC,
∴点C的坐标为(0,﹣3),
又∵OC=3OA,
∴OA=1,
∴点A的坐标为(﹣1,0),
将A、B、C三点坐标代入可得:  ,
,
解得: 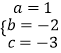 ,
,
故这个二次函数的表达式为:y=x2﹣2x﹣3
(2)
解:在该抛物线上存在点F(2,﹣3),使以点A、C、E、F为顶点的四边形为平行四边形.
理由:由(1)得D(1,﹣4),则直线CD的解析式为:y=﹣x﹣3,
故E点的坐标为(﹣3,0),
∵以A、C、E、F为顶点的四边形为平行四边形,
∴F点的坐标为(2,﹣3)或(﹣2,﹣3)或(﹣4,3),
代入抛物线的表达式检验,只有(2,﹣3)符合.
∴抛物线上存在点F(2,﹣3),使以点A、C、E、F为顶点的四边形为平行四边形
(3)
解:①如图,当直线MN在x轴上方时,设圆的半径为R(R>0),
则N(R+1,R),代入抛物线的表达式,解得R= ![]() ,
,
其中R= ![]() (不合题意,舍去),
(不合题意,舍去),
∴R= ![]() .
.
②如图,当直线MN在x轴下方时,设圆的半径为r(r>0),
则N(r+1,﹣r),
代入抛物线的表达式,解得:r= ![]() ,
,
其中r= ![]() (不合题意,舍去),
(不合题意,舍去),
∴r= ![]() .
.
综合①②得:圆的半径为 ![]() 或
或 ![]() .
.
【解析】(1)分别确定A、B、C的坐标,利用待定系数法可得二次函数的表达式;(2)根据A、C、E、F为顶点的四边形为平行四边形,可得点F的可能坐标,再由点F在抛物线上,可最终确定;(3)分两种情况讨论,①MN在x轴上,②MN在x轴下,表示出N的坐标,代入抛物线解析式可得半斤的长度.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】小明从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:①abc>0;②a﹣b+c<0;③b+2c>0; ④a﹣2b+4c>0;⑤2a=3b
你认为其中正确信息的个数有( )
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图所示,O是直线AB上一点,∠AOC=![]() ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.

(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:扇形DOE的圆心角为直角,它的半径为2cm,正方形OABC内接于扇形,点A、B、C分别在OE、 ![]() 、OD上,过E作EF⊥OE交CB的延长线于F,则图中阴影部分的面积为cm2 .
、OD上,过E作EF⊥OE交CB的延长线于F,则图中阴影部分的面积为cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上对七年级(1)班的8名女生做仰卧起坐测试,若以16次为达标,超过的次数用正数表示,不足的次数用负数表示.现成绩抄录如下:
+2,+2,﹣2,+3,+1,﹣1,0,+1.问:
(1)有几人达标?
(2)平均每人做几次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队为了解运动员的年龄情况,作了一次年龄调查,根据射击运动员的年龄(单位:岁),绘制出如下的统计图.
(1)你能利用该统计图求出平均数、众数和中位数中的哪些统计量?并直接写出结果;
(2)小颖认为,若从该射击队中任意挑选四名队员,则必有一名队员的年龄是15岁.你认为她的判断正确吗?为什么?
(3)小亮认为,可用该统计图求出方差.你认同他的看法吗?若认同,请求出方差;若不认同,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,长方形OABC的边OC,OA分别在x轴和y轴上,点B的坐标是(5,3),直线y=2x+b与x轴交于点E,与线段AB交于点F.
(1)用含b的代数式表示点E,F的坐标;
(2)当b为何值时,△OFC是等腰三角形;
(3)当FC平分∠EFB时,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的中线AF与中位线DE相交于点O。
(1)AF与DE有怎样的关系?为什么?
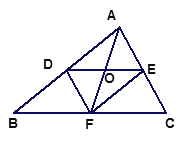
(2)当△ABC满足什么条件时,四边形DFEA是菱形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC. (Ⅰ)求证:直线DM是⊙O的切线;
(Ⅱ)求证:DE2=DFDA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com