
【题目】如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx﹣k的图象的交点坐标为A(m,2).
(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx﹣k的值大于函数y=x的值的自变量x的取值范围.

【答案】(1) m=2; y=2x﹣2;(2) 2;(3) x>2.
【解析】试题分析:(1)先把A(m,2)代入正比例函数解析式可计算出m=2,然后把A(2,2)代入y=kx﹣k计算出k的值,从而得到一次函数解析式为y=2x﹣2;
(2)先确定B点坐标,然后根据三角形面积公式计算;
(3)观察函数图象得到当x>2时,直线y=kx﹣k都在y=x的上方,即函数y=kx﹣k的值大于函数y=x的值.
试题解析:(1)把A(m,2)代入y=x得m=2,则点A的坐标为(2,2),
把A(2,2)代入y=kx﹣k得2k﹣k=2,解得k=2,
所以一次函数解析式为y=2x﹣2;
(2)把x=0代入y=2x﹣2得y=﹣2,则B点坐标为(0,﹣2),
所以S△AOB=![]() ×2×2=2;
×2×2=2;
(3)自变量x的取值范围是x>2.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG. 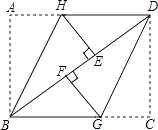
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为285元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六.星期日休市)
星期 | 一 | 二 | 三 | 四 | 五 |
收盘价的变化(与前一天收盘价比较) | +7 | +5 |
|
| +8 |
问:(1)本周星期三黄金的收盘价是多少?
(2)本周黄金收盘时的最高价.最低价分别是多少?
(3)上周,小王以周五的收盘价285元/克买入黄金1000克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金1000克,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律,观察下面算式,解答问题.
1+3 =4 =22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
(1)请猜想1+3+5+7+9+…+19=
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n +1)+(2n +3)=
(3)试计算:101 +103+…+197 +199.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD. 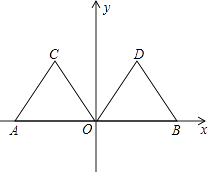
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是个单位长度;△AOC与△BOD关于直线对称,则对称轴是;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是度;
(2)连结AD,交OC于点E,求∠AEO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线y=x向下平移2个单位后和直线y=kx+b(k≠0)重合,直线y=kx+b(k≠0)与x轴交于点A,与y轴交于点B .
(1)请直接写出直线y=kx+b(k≠0)的表达式和点B的坐标;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com