
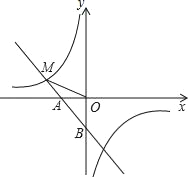
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)当y2>y1时,求x的取值范围;
(3)求点B到直线OM的距离.
【答案】(1)y=﹣![]() ;(2)﹣2<x<0或x>1;(3)
;(2)﹣2<x<0或x>1;(3)![]()
【解析】
(1)先把M(-2,m)代入y=-x-1求出m得到M(-2,1),然后把M点坐标代入y=![]() 中可求出k的值,从而得到反比例函数解析式;
中可求出k的值,从而得到反比例函数解析式;
(2)通过解方程组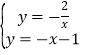 得反比例函数与一次函数的另一个交点坐标为(1,-2),然后写出反比例函数图象在一次函数图象上方所对应的自变量的范围即可;
得反比例函数与一次函数的另一个交点坐标为(1,-2),然后写出反比例函数图象在一次函数图象上方所对应的自变量的范围即可;
(3)设点B到直线OM的距离为h,然后利用面积法得到![]()
![]() h=1,于是解方程即可,
h=1,于是解方程即可,
解:(1)把M(﹣2,m)代入y=﹣x﹣1得m=2﹣1=1,则M(﹣2,1),
把M(﹣2,1)代入y=![]() 得k=﹣2×1=﹣2,
得k=﹣2×1=﹣2,
所以反比例函数解析式为y=﹣![]() ;
;
(2)解方程组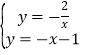 得
得![]() 或
或![]() ,
,
则反比例函数与一次函数的另一个交点坐标为(1,﹣2),
当﹣2<x<0或x>1时,y2>y1;
(3)OM=![]() =
=![]() ,S△OMB=
,S△OMB=![]() ×1×2=1,
×1×2=1,
设点B到直线OM的距离为h,
![]()
![]() h=1,解得h=
h=1,解得h=![]() ,
,
即点B到直线OM的距离为![]() .
.


科目:初中数学 来源: 题型:
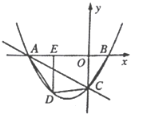
【题目】已知,在平面直角坐标系xOy中,抛物线L:y=x2-4x+3与x轴交于A,B两点(点A在点B的左侧),顶点为C.
(1)求点C和点A的坐标.
(2)定义“L双抛图形”:直线x=t将抛物线L分成两部分,首先去掉其不含顶点的部分,然后作出抛物线剩余部分关于直线x=t的对称图形,得到的整个图形称为抛物线L关于直线x=t的“L双抛图形”(特别地,当直线x=t恰好是抛物线的对称轴时,得到的“L双抛图形”不变),
①当t=0时,抛物线L关于直找x=0的“L双抛图形”如图所示,直线y=3与“L双抛图形”有______个交点;
②若抛物线L关于直线x=t的“L双抛图形”与直线y=3恰好有两个交点,结合图象,直接写出t的取值范围:______;
③当直线x=t经过点A时,“L双抛图形”如图所示,现将线段AC所在直线沿水平(x轴)方向左右平移,交“L双抛图形”于点P,交x轴于点Q,满足PQ=AC时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
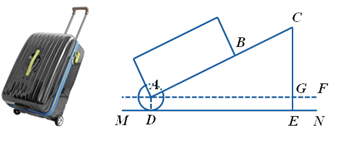
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆![]() 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,![]() =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)如图1,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() 轴相交于点
轴相交于点![]() ,抛物线与
,抛物线与![]() 轴相交于点
轴相交于点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;

(3)如图2,点![]() 是折线
是折线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,直线
轴,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 落在
落在![]() 轴上,请直接写出
轴上,请直接写出![]() 点的坐标.
点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
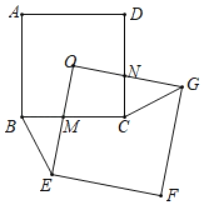
【题目】如图,已知正方形OEFG的顶点O与正方形ABCD的中心O重合,若正方形OEFG绕O点旋转.
(1)探究:在旋转的过程中线段BE与线段CG有什么数量关系及位置关系?证明你的结论;
(2)若正方形ABCD的边长为a,探究:在旋转过程中四边形OMCN的面积是否发生变化?若不变化求其面积,若变化指出变化过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ≈1.7,结果精确到个位).
≈1.7,结果精确到个位).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
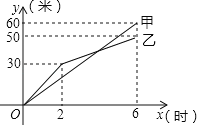
(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2.
(2)求点C1在旋转过程中所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,经过点
,经过点![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为点
轴的另一个交点为点![]() ,点
,点![]() 是抛物线上一点,过点
是抛物线上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当点
当点![]() 在第三象限,设
在第三象限,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;
的坐标;
![]() 连接
连接![]() ,若
,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com