
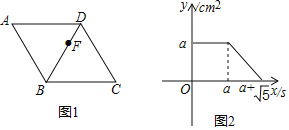
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B。如图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
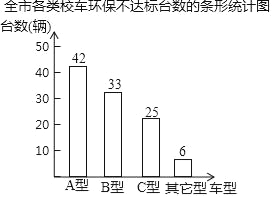
【题目】长春市对全市各类(A型、B型、C型.其它型)校车共848辆进行环保达标普查,普查结果绘制成如下条形统计图:
(1)求全市各类环保不达标校车的总数;
(2)求全市848辆校车中环保不达标校车的百分比;
(3)规定环保不达标校车必须进行维修,费用为:A型500元/辆,B型1000元/辆,C型600元/辆,其它型300元/辆,求全市需要进行维修的环保不达标校车维修费的总和;
(4)若每辆校车乘坐40名学生,那么一次性维修全部不达标校车将会影响全市80000名学生乘校车上学的百分比是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,给出如下定义:已知两个函数,如果对于任意的自变量x,这两个函数对应的函数值记为y1、y2,都有点(x,y1)和(x,y2)关于点(x,x)中心对称(包括三个点重合时),由于对称中心都在直线y=x上,所以称这两个函数为关于直线y=x的特别对称函数.例如:y=![]() x和y=
x和y=![]() 为关于直线y=x的特别对称函数.
为关于直线y=x的特别对称函数.
(1)若y=3x+2和y=kx+t(k≠0)为关于直线y=x的特别对称函数,点M(1,m)是y=3x+2上一点.
①点M(1,m)关于点(1,1)中心对称的点坐标为 .
②求k、t的值.
(2)若y=3x+n和它的特别对称函数的图象与y轴围成的三角形面积为2,求n的值.
(3)若二次函数y=ax2+bx+c和y=x2+d为关于直线y=x的特别对称函数.
①直接写出a、b的值.
②已知点P(﹣3,1)、点Q(2,1),连结PQ,直接写出y=ax2+bx+c和y=x2+d两条抛物线与线段PQ恰好有两个交点时d的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,顽皮的小刚拿着老师的等腰直角三角板放在黑板上画好了的平面直角坐标系内(如图),已知直角顶点H的坐标为(0,1),另一个顶点G的坐标为(4,4),则点K的坐标为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善南宁市的交通现状,市政府决定修建地铁,甲、乙两工程队承包地铁1号线的某段修建工作,从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的3倍;若由甲队先做20天,剩下的工程再由甲、乙两队合作10天完成.
![]() 求甲、乙两队单独完成这项工程各需多少天?
求甲、乙两队单独完成这项工程各需多少天?
![]() 已知甲队每天的施工费用为
已知甲队每天的施工费用为![]() 万元,乙队每天的施工费用为
万元,乙队每天的施工费用为![]() 万元,工程预算的施工费用为500万元,为缩短工期,拟安排甲、乙两队同时开工合作完成这项工程,那么工程预算的施工费用是否够用?若不够用,需增加多少万元?
万元,工程预算的施工费用为500万元,为缩短工期,拟安排甲、乙两队同时开工合作完成这项工程,那么工程预算的施工费用是否够用?若不够用,需增加多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
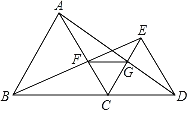
【题目】如图,B、C、D在同一直线上,△ABC和△CDE都是等边三角形,且在直线BD的同侧,连接BE交AC于点F,连接AD交CE于点G,连接FG.
(1)求证:AD=BE;
(2)求证:△ACG≌△BCF;
(3)试猜想△CFG的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com