练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．若想检验一块儿破损的木板的两条直的边缘AB，CD是否平行，你的办法是画一条直线截线段AB与CD，测量一对同位角，如果相等，则AB∥CD，反之，则不平行．（工具不限，可结合图形进行说明，只要能说清思路即可）

    分析 根据同位角相等，两直线平行，或内错角相等，两直线平行，进行解答即可．

    解答 解：根据同位角相等，两直线平行，可以画一条直线截线段AB与CD，测量一对同位角，如果相等，则AB∥CD，反之，则不平行．
    故答案为：画一条直线截线段AB与CD，测量一对同位角，如果相等，则AB∥CD，反之，则不平行．

    点评 本题主要考查了平行线的判定，解题时注意：同位角相等，两直线平行；内错角相等，两直线平行．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．如图1，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连接EB，过点A作AM⊥BE，垂足为M，AM交BD于点F．
    （1）求证：OE=OF；
    （2）如图2，若点E在AC的延长线上，AM⊥BE于点M，交DB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗？如果成立，请给出证明；如果不成立，请说明理由．
    （3）如图3，若点E在CA的延长线上，AM⊥BE于点M，交BD的延长线于点F，请你将图形补充完整，其他条件不变，则结论“OE=OF”还成立吗？
    （提醒：先画图再回答、不需要说明理由；只回答、不画图不得分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．已知∠α=33°54′，则∠α的补角为146°6′．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．$\sqrt{26}$-2的值在（　　）
    A．2、3之间B．3、4之间C．5、6之间D．6、7之间

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．在一个m（m≥3，m为整数）位的正整数中，若从左到右第n（n≤m，n为正整数）位上的数字与从右到左第n位上的数字之和都等于同一个常数k（k为正整数），则称这样的数为“对称等和数”．例如在正整数3186中，因为3+6=1+8=9，所以3186是“对称等和数”，其中k=9．再如在正整数53697中，因为5+7=3+9=6+6=12，所以53697是“对称等和数”，其中k=12．
    （1）已知在一个能被11整除的四位“对称等和数”中k=4．设这个四位“对称等和数”的千位上的数字为s（1≤s≤9，s为整数），百位上的数字为t（0≤t≤9，t为整数），$\frac{st}{2}$是整数，求这个四位“对称等和数”；
    （2）已知数A，数B，数C都是三位“对称等和数”．A=$\overline{1a5}$（1≤a≤9，a为整数），设数B十位上的数字为x（0≤x≤9，x为整数），数C十位上的数字为y（0≤y≤9，y为整数），若A+B+C=1800，求证：y=-x+15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．观察下列等式：
    ①32-4×12=5；②52-4×22=9；③72-4×32=13；…
    根据上述式子的规律，解答下列问题：
    （1）第④个等式为92-4×42=17；
    （2）写出第n个等式，并说明其正确性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

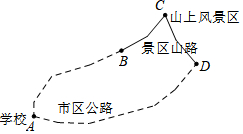    14．为了提倡“原色青春，绿色行走！”，某市某校组织学生从学校（点A）出发，沿A→B→C→D→A的路线参加总路程为14km绿色行走活动，其中路线A→B段、D→A段是我市区公路，B→C段、C→D段是景区山路．已知学生队伍在市区公路的行进速度为6km/h，在景区山路的行进速度为2km/h，本次行走共用3.5h．问本次行走活动中市区公路、景区山路各多少km？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，∠1=13°，∠AOC=90°，点B、O、D在同一直线上，则∠2的度数为103°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列事件中，必然事件是（　　）
    A．掷一枚硬币，正面朝上
    B．从2、4、6、8、10这5张卡片中任抽一张是奇数
    C．a是实数，|a|≥0
    D．从车间刚生产的产品中任意抽取一件，是次品

    查看答案和解析>>

    同步练习册答案