

分析 (1)首先根据∠ACB=90°,AC=BC,可得∠BAC=∠ABC=45°;然后根据三角形的外角的性质,可得∠FDQ=∠FAB+∠ABC=∠FAB+45°;最后在△BPQ中,根据三角形的内角和定理,推得∠FQD=∠BQP=∠FAB+45°,即可推得∠FDQ=∠FQD,根据等腰三角形的判定即可得到结论;
(2)MN与EN的数量关系是:MN=3EN.首先判断出AH∥DG∥PQ,推得$\frac{BP}{PA}$=$\frac{BQ}{QH}$,再根据相似三角形判定的方法,判断出△APC∽△BPQ,推得$\frac{BP}{PA}$=$\frac{BQ}{AC}$=$\frac{BQ}{BC}$,进一步推得BQ=HC=CD;然后判断出AH∥PF,推得$\frac{DQ}{DH}=\frac{FD}{AD}=\frac{GQ}{AD}=\frac{BQ}{BD}$,进一步推得DQ=CD,BP=PG,再根据BI∥GQ,推得BI=GM;最后判断出AD∥BI,即可推得$\frac{DE}{BI}=\frac{CD}{BC}=\frac{1}{3}$,据此判断出MN=3EN即可.
解答 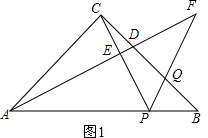 解:(1)FQ=FO,
解:(1)FQ=FO,
理由:如图1,
∵∠ACB=90°,AC=BC,
∴∠BAC=∠ABC=45°,
由三角形的外角的性质,可得
∠FDQ=∠FAB+∠ABC=∠FAB+45°,
∵AD⊥PC,
∴∠AEP=90°,
∴∠FAB+∠APC=90°,
∴∠APC=90°-∠FAB,
又∵∠BPQ=∠APC,
∴∠BPQ=90°-∠FAB,
∴∠FQD=∠BQP=180°-∠BPQ-∠ABC
=180°-(90°-∠FAB)-45°
=∠FAB+45°
∴∠FDQ=∠FQD,
∴FQ=FO;
(2)如图2,延长DC至H,使HC=CD,连接AH,过点B作BI∥GQ,交CP延长线于点I,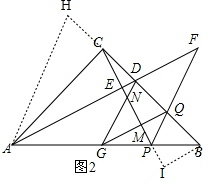 ,
,
∵HC=CD,AC⊥HD,
∴△ADH是等腰三角形,
∴AD=AH,
∴∠H=∠ADH=∠FDQ=∠FQD=∠BQP,
∵把△DFQ沿DQ边翻折,得到△DGQ,
∴△GDQ≌△FDQ,
∴∠FDQ=∠GDQ,
又∵∠H=∠FDQ=∠BQP,
∴∠H=∠BQP=∠GDQ,
∴AH∥DG∥PQ,
∴$\frac{BP}{PA}$=$\frac{BQ}{QH}$,∠GQP=∠DGQ,
在△APC和△BPQ中,
$\left\{\begin{array}{l}{∠APC=∠BPQ}\\{∠CAP=∠QBP=45°}\end{array}\right.$,
∴△APC∽△BPQ,
∴$\frac{BP}{PA}$=$\frac{BQ}{AC}$=$\frac{BQ}{BC}$,
又∵$\frac{BP}{PA}$=$\frac{BQ}{QH}$,
∴$\frac{BQ}{BC}$=$\frac{BQ}{QH}$,
∴BC=QH,
∴BQ=HC,
又∵HC=CD,
∴BQ=HC=CD.
∵把△DFQ沿DQ边翻折,得到△DGQ,
∴∠DFQ=∠DGQ,
又∵∠GQP=∠DGQ,
∴∠GQP=∠DFQ,
∴AD∥GQ,四边形DFQG是平行四边形,
∴$\frac{MN}{EN}$=$\frac{GM}{DE}$,FD=GQ,
∵AH∥PF,
∴$\frac{DQ}{DH}=\frac{FD}{AD}=\frac{GQ}{AD}=\frac{BQ}{BD}$,
又∵DH=2CD,BQ=CD,
∴$\frac{DQ}{2CD}$=$\frac{CD}{BD}$,
∴$\frac{DQ}{2CD}$=$\frac{CD}{CD+DQ}$,
∴(DQ+2CD)(DQ-CD)=0,
解得DQ=CD,或DQ=-2CD(舍去),
∵$\frac{BP}{PG}$=$\frac{BQ}{DQ}$=1,
∴BP=PG,
∵BI∥GQ,
∴$\frac{BI}{GM}$=$\frac{BP}{PG}$=1,
∴BI=GM,
∵BI∥GQ,AD∥GQ,
∴AD∥BI,
∴$\frac{DE}{BI}$=$\frac{CD}{BC}$=$\frac{1}{3}$,
∴$\frac{DE}{GM}$=$\frac{1}{3}$,
∴$\frac{MN}{EN}$=$\frac{1}{3}$,
∴$\frac{m}{n}$=$\frac{1}{3}$.
点评 此题还考查了平行线的性质和应用,三角形相似的判定和性质的应用,等腰三角形的判定与性质,平行线分线段成比例定理,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
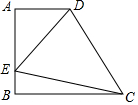 如图,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
如图,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com