
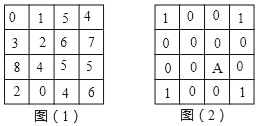
【题目】在图(1)中,对任意相邻的上下或左右两格中的数字同时加1或减2,这算作一次操作,经过若干次操作后,图(1)能变为图(2),则图(2)中A格内的数是_____
【答案】4.
【解析】
每次变换都是在相邻的两格,则将相邻的两格区分出来,如解答中图的有阴影和无阴影.由题可知,每次变换都是阴影格中的一个数据和无阴影格中的一个数据同时加1或减2,所以无论变换多少次,所有阴影格中的数字之和与所有无阴影格中的数字之和的差不变.
解:如图,将相邻两格用阴影区分出来.

由于每次变换都是一个阴影格和相邻的无阴影格中的数据同时加1或减2,所以变换过程中,所有阴影格中的数字之和与所有无阴影格中的数字之和的差不变.
图(1)中对应的阴影格的数字之和为:0+5+2+7+8+5+0+6=33,
图(1)中对应的无阴影格的数字之和为:1+4+3+6+4+5+2+4=29,
图(2)中对应的阴影格的数字之和为:1+A+1=2+A,
图(2)中对应的无阴影格的数字之和为:1+1=2,
由上述分析可知:33-29=2+A-2,
则可得A=4.
故答案为:4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】世界读书日,新华书店矩形购书优惠活动:①一次性购书不超过100元,不享受打折优惠;②一次性购书超过100元但不超过200元一律八折;③一次性购书200元以上一律打六折.小丽在这次活动中,两次购书总共付款190.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A. 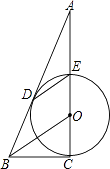
(1)求证:直线BC是⊙O的切线;
(2)若AE=2,tan∠DEO= ![]() ,求AO的长.
,求AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A(0,8),B(6,0),点C(3,a)在线段AB上.
(1)则a的值为________;
(2)若点D(-4,3),求直线CD的函数表达式;
(3)点(-5,-4)在直线CD上吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
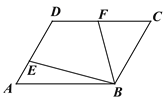
【题目】如图,□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°,若AE=2,FC=3,则EF的长度为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OM上有三点A、B、C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O出发,沿OM方向以1cm/秒的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动,两点同时出发,当点Q运动到点O时,点P、Q停止运动.
(1)若点Q运动速度为2cm/秒,经过多长时间P、Q两点相遇?
(2)当P在线段AB上且PA=3PB时,点Q运动到的位置恰好是线段AB的三等分点,求点Q的运动速度;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知直线 AB、CD 相交于点 O,∠COE=90°
(1)若∠AOC=36°,求∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE 的度数.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835590144/STEM/dc8ee683cff64dfdb92368e07f9f9b9d.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“希望学校”修建了一栋4层的教学大楼,每层楼有6间教室,进出这栋大楼共有3道门(两道大小相同的正门和一道侧门).安全检查中,对这3道门进行了测试:当同时开启一道正门和一道侧门时,2分钟内可以通过400名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%.安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离.假设这栋教学大楼每间教室最多有45名学生,问:建造的这3道门是否符合安全规定?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com