
【题目】如图,PA=PB,∠PAM+∠PBN=180°,求证:OP平分∠AOB.

科目:初中数学 来源: 题型:
【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.

(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:△MNC是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备组织七年级160名学生参加社会实践活动,租用35座和45座两种客车共四辆,每种客车至少租1辆,可以坐不满.
(1)参加本次活动至少需几辆45座客车?
(2)如果35座客车的租金为每辆300元,45座客车的租金为每辆400元,要想使全部租车的费用不超过1550元,则有几种租车的方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
(1)图1中,小明发现DG=BE,请你帮他说明理由.
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.

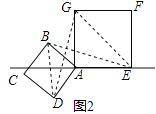

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥BC,垂足为C,AC=2cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_____秒时,△BCA与点P、N、B为顶点的三角形全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织七年级学生体育健康抽测,(1)班25名学生的成绩(满分为100分)统计如下:
90,74,88,65,98,76,81,42,85,70,55,80,95,88,72,87,61,56,76,66,78,72,82,63,100.
(1)90分及以上为A级,75-89分为B级,60-74分为C级,60分以下为D级,请把下面表格补充完整,并将图中的条形图补充完整;
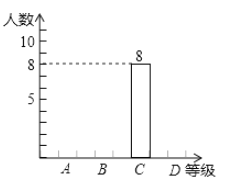
等级 | A | B | C | D |
人数 | 8 |
(2)该校七年级共有1000名学生,如果60分以上为合格,请估计七年级有多少人合格?
(3)请选择合适的统计图表示出抽测中每一个等级的人数占总人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技与经济的发展,中国廉价劳动力的优势开始逐渐消失,而作为新兴领域的机器人产业则迅速崛起,机器人自动化线的市场也越来越大,并且逐渐成为自动化生产线的主要方式,某化工厂要在规定时间内搬运1200千元化工原料.现有A,B两种机器人可供选择,已知A型机器人比B型机器人每小时多搬运30千克,A型机器人搬运900千克所用的时间与B型机器人搬运600千克所用的时间相等.


(1)两种机器人每小时分别搬运多少化工原料?
(2)该工厂原计划同时使用这两种机器人搬运,工作一段时间后,A型机器人又有了新的搬运任务,但必须保证这批化工原料在11小时内全部搬运完毕.求:A型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com