
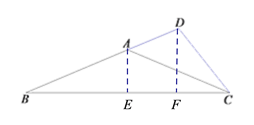
【题目】如图,在等腰三角形ABC中,AB=AC,点D在BA的延长线上,BC=24, ![]() .
.
(1)求AB的长;
(2)若AD=6.5,求![]() 的余切值.
的余切值.

【答案】(1)13(2)![]()
【解析】试题分析:
(1)过点A作AE⊥BC于点E,结合AB=AC,BC=24可得BE=12,在Rt△AEB中,由sin∠ABC=![]() 设AE=5k,AB=13k,由勾股定理可得解得BE=12k=12,由此可得k=1,从而可得AB=13;
设AE=5k,AB=13k,由勾股定理可得解得BE=12k=12,由此可得k=1,从而可得AB=13;
(2)过点D作DF⊥BC于点F,则易得BD=19.5,AE∥DF,从而可得![]() 结合AE=5,BE=12,AB=13即可求得DF=
结合AE=5,BE=12,AB=13即可求得DF=![]() ,BF=18,由此可得CF=BC-BF=6,结合∠DFC=90°即可得到cot∠DCB=
,BF=18,由此可得CF=BC-BF=6,结合∠DFC=90°即可得到cot∠DCB=![]() .
.
试题解析:
(1)过点A作AE⊥BC,垂足为点E,
∵AB=AC,
∴BE=![]() BC=12,
BC=12,
在Rt△ABE中,∠AEB=90°,sin∠ABC=![]() ,
,
设AE=5k,AB=13k,∵AB2=AE2+BE2,
∴169k2=25k2+BE2,解得BE=12K=12,
∴k=1,
∴AE=5,AB=13;
(2)过点D作DF⊥BC,垂足为点F,
∵AD=6.5,AB=13,
∴BD=AB+AD=19.5,
∵AE⊥BC,DF⊥BC ,
∴ ∠AEB=∠DFB=90°,
∴AE∥DF,
∴![]() ,
,
又 ∵ AE=5,BE=12,AB=13,
∴DF=![]() ,BF=18,
,BF=18,
∴CF=BC=BF=6,
∵在Rt△DCF中,∠DFC=90°,
∴cot∠DCB=![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有![]() 本,最多的有
本,最多的有![]() 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:
本数(本) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|

(![]() )统计图表中的
)统计图表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.
(![]() )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.
(![]() )若该校八年级共有
)若该校八年级共有![]() 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读![]() 本及以上的人数.
本及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校八年级150名女生的身高情况,从中随机抽取10名女生,测得身高并绘制如下条形统计图.
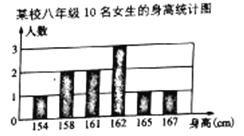
(1)求出这10名女生的身高的中位数和众数;
(2)依据样本估计该校八年级全体女生的平均身高;
(3)请你根据这个样本,在该校八年级中,设计一个挑选50名女生组成方队的方案(要求选中女生的身高尽可能接近).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的距离CD=2.8米,一楼到地平线的距离BC=1米.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1米)
(2)如果给该商场送货的货车高度为2.5米,那么按这样的设计能否保证货车顺利进入地下停车场?请说明理由.(参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)

查看答案和解析>>
科目:初中数学 来源: 题型:
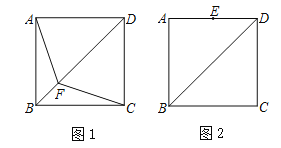
【题目】已知:如图,正方形ABCD中,点F是对角线BD上的一个动点.
(1)如图1,连接AF,CF,直接写出AF与CF的数量关系;
(2)如图2,点E为AD边的中点,当点F运动到线段EC上时,连接AF,BE相交于点O.
①请你根据题意在图2中补全图形;
②猜想AF与BE的位置关系,并写出证明此猜想的思路;
③如果正方形的边长为2,直接写出AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
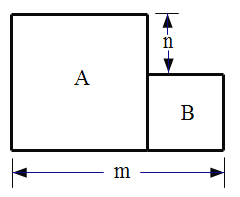
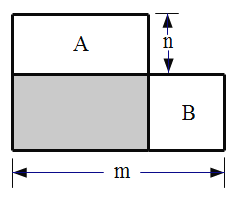
【题目】已知A、B两个边长不等的正方形纸片并排放置(如图所示)
(1)若m=8,n=3,则甲、乙两个正方形纸片的面积之和为: ______________
(2)用m、n表示甲、乙两个正方形纸片的面积之和为:___________________
(3)若A、B两个正方形纸片的面积之和为:![]() ,且右下图中阴影部分的面积为:
,且右下图中阴影部分的面积为:![]() ,则m=___________n=_______________________
,则m=___________n=_______________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com