
 如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )| A. | (-2,1) | B. | (-1,2) | C. | ($\sqrt{3}$,-1) | D. | (-$\sqrt{3}$,1) |
分析 首先过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E,易证得△AOE≌△OCD(AAS),则可得CD=OE=1,OD=AE=$\sqrt{3}$,继而求得答案.
解答 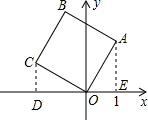 解:过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E,
解:过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E,
则∠ODC=∠AEO=90°,
∴∠OCD+∠COD=90°,
∵四边形OABC是正方形,
∴OC=OA,∠AOC=90°,
∴∠COD+∠AOE=90°,
∴∠OCD=∠AOE,
在△AOE和△OCD中,
$\left\{\begin{array}{l}{∠AEO=∠ODC}\\{∠AOE=∠OCD}\\{OC=AO}\end{array}\right.$,
∴△AOE≌△OCD(AAS),
∴CD=OE=1,OD=AE=$\sqrt{O{A}^{2}-O{E}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴点C的坐标为:(-$\sqrt{3}$,1).
故选D.
点评 此题考查了正方形的性质、全等三角形的判定与性质以及勾股定理.注意准确作出辅助线、证得△AOE≌△OCD是解此题的关键.


科目:初中数学 来源: 题型:选择题
 如图,△ABC经过平移得到△DEF,其中A点(-2,4)平移到D点(2,2),则B点(a,b)平移后的对应点E的坐标是( )
如图,△ABC经过平移得到△DEF,其中A点(-2,4)平移到D点(2,2),则B点(a,b)平移后的对应点E的坐标是( )| A. | (a+2,b) | B. | (a+4,b-2) | C. | (a+2,b-2) | D. | (a+4,b+2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a<3b | B. | $-\frac{1}{3}$a>-$\frac{1}{3}$b | C. | a-3<b-3 | D. | a+1<b-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我国水资源比较缺乏,人均水量约为世界人均水量的四分之一,其中西北地区缺水尤为严重.一村民为了蓄水,他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水.已知白铁皮的长为280cm,宽为160cm(如图).
我国水资源比较缺乏,人均水量约为世界人均水量的四分之一,其中西北地区缺水尤为严重.一村民为了蓄水,他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水.已知白铁皮的长为280cm,宽为160cm(如图).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com