
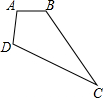
 如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.分析 (1)相等.连接AC,根据SSS证明两个三角形全等即可.
(2)由勾股定理求出AC,再根据三角形三边的关系求出AD的取值范围.
(3)分两种情形①当点C在点D右侧时,②当点C在点D左侧时,分别列出方程组即可解决问题,注意最后理由三角形三边关系定理,检验是否符合题意.
解答 解:(1)相等.
理由:连接AC,
在△ACD和△ACB中,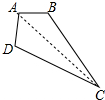
$\left\{\begin{array}{l}{AC=AC}\\{AD=AB}\\{CD=BC}\end{array}\right.$,
∴△ACD≌△ACB,
∴∠B=∠D.
(2)∵AB=2cm,BC=5cm,且∠B=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$
根据三角形三边关系可知$\sqrt{29}$-5≤AD≤$\sqrt{29}$+5
所以AD可以为5cm.
(3)设AD=x,BC=y,
当点C在点D右侧时,$\left\{\begin{array}{l}{x+2=y+5}\\{x+(y+2)+5=30}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=13}\\{y=10}\end{array}\right.$,
当点C在点D左侧时,点C在D左侧时,三边之和等于第四边是构不成四边形的,不合题意,
综上所述,AD=13cm,BC=10cm.
点评 本题考查全等三角形的判定和性质、二元一次方程组、三角形三边关系定理等知识,解题的关键是学会分类讨论,考虑问题要全面,属于中考常考题型.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(-3)和3 | B. | -3和|-3| | C. | -3和$\frac{1}{3}$ | D. | $\sqrt{3}$和$\frac{1}{\sqrt{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com