
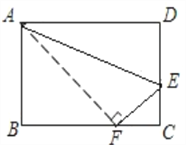
【题目】如图,把长方形沿AE对折后点D落在BC边的点F处,BC=5cm,
AB=4cm,求:(1)CF的长;(2)EF的长.

【答案】(1)2 cm;(2)2.5cm
【解析】
试题(1)由折叠的性质可得AF=AD,在Rt△ABF中根据勾股定理可求得BF的长,利用CF=BC-BF即可求得答案;(2)在Rt△CEF中,设EF=x m,则CE=(4-x) m ,根据勾股定理列方程,解方程即可.
试题解析:
(1)∵四边形ABCD是长方形,
∴AD=AB=4、AD=BC=5、∠B=∠C=900 ,
∵长方形沿AE对折后点D落在BC边的F处,
∴△ADE![]() △AFE,
△AFE,
∴DE=EF, AF=AD=5
在Rt△ABF中,有AB2+BF2=AF2,
BF=![]() =3,
=3,
∴ CF=BC-BF=2 ;
(2)由(1)知:BC=AD=5、DE=EF
在Rt△CEF中,设EF=x m,则CE=(4-x) m
由勾股定理得:CF2+CE2=EF2
22+(4-x)2=x2
4+16-8x+x2=x2
8x=20
x=2.5
即:EF=2.5 m


科目:初中数学 来源: 题型:
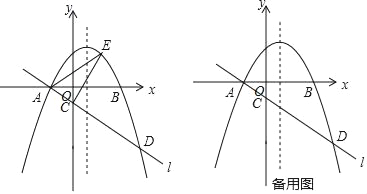
【题目】如图,在平面直角坐标系中,直线l:y=kx+h与x轴相交于点A(﹣1,0),与y轴相交于点C,与抛物线y=﹣x2+bx+3的一交点为点D,抛物线过x轴上的AB两点,且CD=4AC.
(1)求直线l和抛物线的解析式;
(2)点E是直线l上方抛物线上的一动点,求当△ADE面积最大时,点E的坐标;
(3)设P是抛物线对称轴上的一点,点Q在抛物线上,四边形APDQ能否为矩形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b交x轴于点A(1,0),与双曲线y=-![]() (x<0)交于点B(-1,a).
(x<0)交于点B(-1,a).
(1)求直线AB的解析式;
(2)若点B左侧一直线x=m与直线AB交于点C,与双曲线交于点D(C、D两点不重合),当BC=BD时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
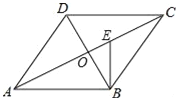
【题目】如图,在ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:AC⊥BD;
(2)若AB=14,cos∠CAB=![]() ,求线段OE的长.
,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四条直线l1:y1=![]() x,l2:y2=
x,l2:y2=![]() x,l3:y3=﹣
x,l3:y3=﹣![]() x,l4:y4=﹣
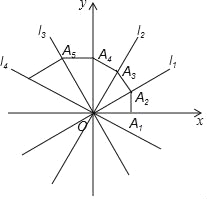
x,l4:y4=﹣![]() ,OA1=l,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l3交y轴于点A4…,则点A2坐标为_____;点A2018的坐标为_____.
,OA1=l,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l3交y轴于点A4…,则点A2坐标为_____;点A2018的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,分别是两棵树及其影子的情形
(1)哪个图反映了阳光下的情形?哪个图反映了路灯下的情形.
(2)请画出图中表示小丽影长的线段.
(3)阳光下小丽影子长为1.20m树的影子长为2.40m,小丽身高1.88m,求树高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将4筐杨梅每筐以5千克为基准,超过的千克数记为正数,不足的千克数记为负数,记录如图.
⑴这4筐杨梅最重的比最轻的多多少千克?
⑵这4筐杨梅总重量是多少千克?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.

(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com