
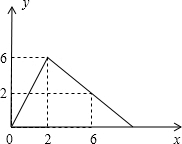
 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:
某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:
|
|

|
|


科目:初中数学 来源: 题型:
| x | 0 | 0.5 | 1 | 1.1 | 1.2 | 1.3 |
| y | -15 | -8.75 | -2 | -0.59 | 0.84 | 2.29 |
查看答案和解析>>
科目:初中数学 来源: 题型:
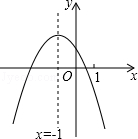 二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:| A、4个 | B、3个 | C、2个 | D、1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
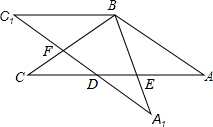 在△ABC中,AB=BC=4,∠ABC=120°,将△ABC绕点B旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
在△ABC中,AB=BC=4,∠ABC=120°,将△ABC绕点B旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.查看答案和解析>>
科目:初中数学 来源: 题型:
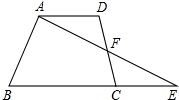 四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.
四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
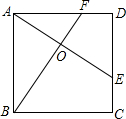 如图,E、F分别是正方形的边CD、AD上的点,且CE=DF,AE、BF交于点O,下列结论正确的个数为( )
如图,E、F分别是正方形的边CD、AD上的点,且CE=DF,AE、BF交于点O,下列结论正确的个数为( ) | A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com