
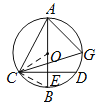
【题目】如图, ![]() 为⊙
为⊙![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,点
,点![]() 是
是![]() 上一点,连结
上一点,连结![]() ,
, ![]() .
.
(![]() )在下添辅助线的前提下直接写出图中与
)在下添辅助线的前提下直接写出图中与![]() 相等的角,不用证明.
相等的角,不用证明.
(![]() )求证:当
)求证:当![]() 时,
时, ![]() 与
与![]() 相似.
相似.
(![]() )若
)若![]() ,求
,求![]() 的度数.
的度数.
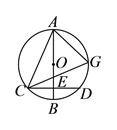
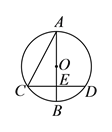
【答案】(1)![]() ;(2)答案见解析;(3)60°.
;(2)答案见解析;(3)60°.
【解析】试题分析:(1)结论:∠ACE=∠AGC.首先证明AB垂直平分CD,推出AC=AD,∠ACD=∠ADC,因为∠AGC=∠ADC,由此即可证明.
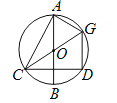
(2)如图2中,由DG∥AB,推出∠AEC=∠CDG=90°,推出CG是直径,推出∠CAG=90°,由此即可证明.
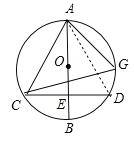
(3)如图3中,连接OC、BC.只要证明△OBC是等边三角形即可解决问题.
试题解析:解:(![]() )结论:∠ACE=∠AGC.理由如下:
)结论:∠ACE=∠AGC.理由如下:
如图1中,连接AD.
∵AB是直径,AB⊥CD,∴EC=ED,∴AD=AC,∴∠ACE=∠ADC.
∵∠AGC=∠ADC,∴∠ACE=∠AGC.
(![]() )证明:∵
)证明:∵![]() ,
,
∴![]() ,
,
∴![]() 也是直径,
也是直径,
∴![]() ,
, ![]() ,
,
∴![]() .
.
(![]() )如图,连接
)如图,连接![]() ,
, ![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
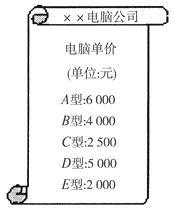
【题目】如图,某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写出所有选购方案(利用树状图或列表方法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(3)现知希望中学用10万元购买甲、乙两种品牌电脑共36台(价格如图所示),其中甲品牌电脑为A型号电脑,求购买的A型号电脑有多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测倾器测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.则河的宽度为________米(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲袋里装有红球5个,白球2个和黑球12个,乙袋里装有红球20个,白球20个和黑球10个.
(1)如果你想取出1个黑球,选哪个袋子成功的机会大?请说明理由.
(2)某同学说“从乙袋取出10个红球后,乙袋中的红球个数仍比甲袋中红球个数多,所以此时想取出1个红球,选乙袋成功的机会大.”你认为此说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DBC都是边长为2的等边三角形.

(1)以图1中的某个点为旋转中心,旋转△DBC,就能使△DBC与△ABC重合,则满足题意的点为: (写出符合条件的所有点);
(2)将△DBC沿BC方向平移得到△D1B1C1,如图2、图3,则四边形ABD1C1是平行四边形吗?证明你的结论;
(3)在(2)的条件下,当BB1= 时,四边形ABD1C1为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C分别在函数![]() 的图像上,AB∥x轴,AC∥y轴,已知点A的坐标为(2,m)(
的图像上,AB∥x轴,AC∥y轴,已知点A的坐标为(2,m)(![]() ),延长OA交反比例函数
),延长OA交反比例函数![]() 的图像交于点P,
的图像交于点P,
(1)当点P横坐标为3,求m的值;
(2)连接CO,当AC=OA时,求m的值;
(3)连接BP、CP,![]() 的值是否随m的变化而变化?若变化,说明理由;若不变,求出
的值是否随m的变化而变化?若变化,说明理由;若不变,求出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、 B的坐标分别为(0,2),(1,0),直线y=![]() x3与y轴交于点C, 与x轴交于点D,
x3与y轴交于点C, 与x轴交于点D,

(1)求直线AB与CD交点E的坐标;
(2)求四边形OBEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com