
【题目】下列运算正确的是( )
A.x4+x4=x8
B.(x﹣y)2=x2﹣y2
C.x3x4=x7
D.(2x2)3=2x6
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.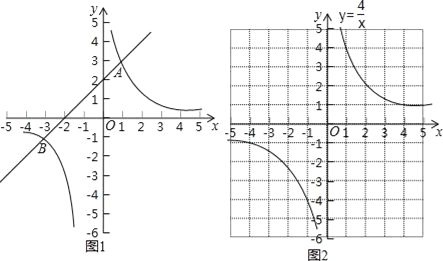
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1>![]() ;
;
当x<0时,原不等式可以转化为x2+4x﹣1<![]() ;
;
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
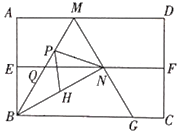
【题目】如图,四边形是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①∠ABN= 60°;②AM=1;③![]() ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是
;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是![]() .其中正确结论的序号是___________.
.其中正确结论的序号是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,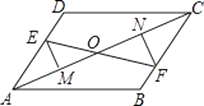
求证:
(1)EM=FN;
(2)EF与MN互相平分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题14分)如图,点A和动点P在直线![]() 上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线
上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线![]() ⊥
⊥![]() ,过点O作OD⊥
,过点O作OD⊥![]() 于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=
于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=![]() CD,以DE,DF为邻边作矩形DEGF,设AQ=
CD,以DE,DF为邻边作矩形DEGF,设AQ=![]()
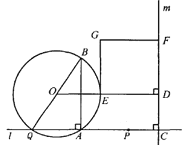
(1)用关于![]() 的代数式表示BQ,DF;
的代数式表示BQ,DF;
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于另一点N,若BN的弦心距为1,求AP的长(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店将原来每件m元的服装加价50%后销售,由于转季,服装店将该服装降价40%,则经过降价后每件服装的价格为元(结果用含m的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com