练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：|﹣2|+2sin30°﹣（﹣ ）2+（tan45°）﹣1 ．

    【答案】解：原式=2+1﹣3+1=1
    【解析】本题涉及绝对值、负整数指数幂、特殊角的三角函数值、二次根式化简四个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．
    【考点精析】利用整数指数幂的运算性质和特殊角的三角函数值对题目进行判断即可得到答案，需要熟知aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y= （m≠0）的图象交于A，B两点，与x轴交于C点，与y轴交于D点；点A的坐标为（n，6），点C的坐标为（﹣2，0），且tan∠ACO=2．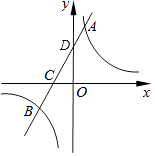
    （1）求该反比例函数和一次函数的解析式；
    （2）求点B的坐标；
    （3）求△AOB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：在数学课上，老师给同学们布置了一道尺规作图题： 尺规作图：作Rt△ABC，使其斜边AB=c，一条直角边BC=a．已知：如图1，正比例函数和反比例函数的
    图象分别交于M、N两点．
    要求：在y轴上求作点P，使得∠MPN为直角．
    小丽的作法如下：如图2，以点O为圆心，以OM长为半径作⊙O，
    ⊙O与y轴交于P1、P2两点，则点P1、P2即为所求．
    老师说：“小丽的作法正确．”
    请回答：小丽这样作图的依据是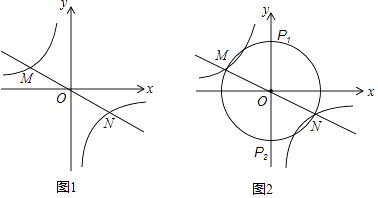

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为1个单位长度的小正方形组成的网格中．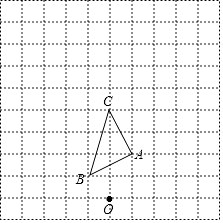
    （1）以图中的点O为位似中心，在网格中画出△ABC的位似图形△A1B1C1 ， 使△A1B1C1与△ABC的位似比为2：1；
    （2）若△A1B1C1的面积为S，则△ABC的面积是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点A（10，0），B（4，8），C（0，8），连接AB，BC，点P在x轴上，从原点O出发，以每秒1个单位长度的速度向点A运动，同时点M从点A出发，以每秒2个单位长度的速度沿折线A﹣B﹣C向点C运动，其中一点到达终点时，另一点也随之停止运动，设P，M两点运动的时间为t秒．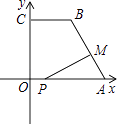

    （1）求AB长；
    （2）设△PAM的面积为S，当0≤t≤5时，求S与t的函数关系式，并指出S取最大值时，点P的位置；
    （3）t为何值时，△APM为直角三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】鄂州市化工材料经销公司购进一种化工原料若干千克，价格为每千克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时，y=80；x=50时，y=100．在销售过程中，每天还要支付其他费用450元．
    （1）求出y与x的函数关系式，并写出自变量x的取值范围．
    （2）求该公司销售该原料日获利w（元）与销售单价x（元）之间的函数关系式．
    （3）当销售单价为多少元时，该公司日获利最大？最大获利是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D是AC边上一点，且AD=2DC，E是AB边上一点，ED与BC的延长线相交于点F，且BC=CF，G是EF的中点，连接CG，若CG=2，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知锐角△ABC中，边BC长为12，高AD长为8．
    （1）如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K．
    ①求 的值；
    ②设EH=x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值；
    （2）若AB=AC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，直接写出正方形PQMN的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一三角形的三边长分别为5、12、13，则此三角形的内切圆半径为 ．

    查看答案和解析>>

    同步练习册答案