练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （1）计算： ;

    （2）化简： .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．如图，△ABC的外角∠ACD的平分线：CP与内角∠ABC平分线BP交于点P，若∠A=60°，求∠P的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，△ABC是⊙O的内接三角形，若∠OBC=70°，则∠A的度数是20°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知：如图，△ABC中，∠ACB=90°，F为AB的中点，EF⊥AB，求证：△CDF∽△ECF．

    查看答案和解析>>

    科目：初中数学 来源：2017届江苏省扬州市九年级下学期第一次月考数学试卷（解析版） 题型：判断题

    某学校准备组织部分学生到少年宫参加活动，陈老师从少年宫带回来两条信息：

    信息一：按原来报名参加的人数，共需要交费用320元，如果参加的人数能够增加到原来人数的2倍，就可以享受优惠，此时只需交费用480元；

    信息二：如果能享受优惠，那么参加活动的每位同学平均分摊的费用比原来少4元．

    根据以上信息，原来报名参加的学生有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，已知四边形ABCD内接于⊙O，直径AC=6，对角线AC、BD交于E点，且AB=BD，EC=1，则AD的长是$\frac{3\sqrt{15}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

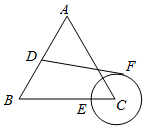    10．如图，等边△ABC的边长为4，D、E是边AB、BC上的动点（与A、B不重合），AD=2CE，以CE的长为半径作⊙C，DF与⊙C相切于F，下列关于DF的长说法正确的是（　　）
    A．有最大值，无最小值B．有最小值，无最大值
    C．有最大值，也有最小值D．为定值

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．图1是边长分别为4$\sqrt{3}$和2的两个等边三角形纸片ABC和OD′E′叠放在一起（C与O重合）．
    （1）操作：固定△ABC，将△ODE绕点C顺时针旋转30°，后得到△ODE，连接AD、BE、CE的延长线交AB于F（图2）：
    探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
    （2）在（1）的条件下将△ODE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR，当点P与点F重合时停止运动（图3）．
    探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
    （3）将图1中△ODE固定，把△ABC沿着OE方向平移，使顶点C落在OE的中点G处，设为△ABG，然后奖△ABG绕点G顺时针旋转，边BG交边DE于点M，边AG交边DO于点N，设∠BGE=α（30°＜α＜90°）（图4）．
    探究：在图4中，线段ON•EM的值是否随α的变化而变化？如果没有变化，请你求出ON•EM的值，如果有变化，请你说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

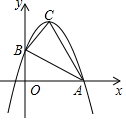    8．如图，已知抛物线y=ax2+bx+c与x轴的一个交点为A（3，0），与y铀的交点为B（0，3），其顶点为C，对称轴为x=1．
    （1）求抛物线的解析式；
    （2）判断△ABC的形状；
    （3）已知点M为线段AB上方抛物线上的一个动点，请写出△ABM面积关系式，并求出当△ABM面积最大时点M的坐标．

    查看答案和解析>>

    同步练习册答案