
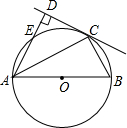
 证明与计算.
证明与计算.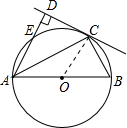 连接OC,
连接OC,| AB2-BC2 |
| 3 |
| 1 |
| 2 |
| 3 |


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
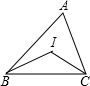 实践与探索!如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数,
实践与探索!如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数,查看答案和解析>>
科目:初中数学 来源: 题型:
 作图、证明与计算
作图、证明与计算查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
![]()

(1)满足什么条件时,四个小朋友所站点为顶点的四边形A1B1C1D1是正方形?(只写探究出的结论)
(2)要使四边形A1B1C1D1是正方形,且面积为大正方形ABCD面积的![]() ,则四个小朋友应站在各边的什么位置上?(写出证明与计算过程)
,则四个小朋友应站在各边的什么位置上?(写出证明与计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
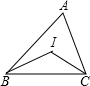 实践与探索!如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数,
实践与探索!如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com