
分析 由|ab-2|+(b-1)2=0可求出a与b的值,然后将所求的式子进行化简后代入求值即可.
解答 解:由题意可知:ab-2=0,b-1=0,
∴a=2,b=1
∵$\frac{1}{(n+2)(n+1)}$=$\frac{(n+2)-(n+1)}{(n+2)(n+1)}$=$\frac{1}{n+1}$-$\frac{1}{n+2}$
∴原式=$\frac{1}{2×1}$+$\frac{1}{(2+1)(2+2)}$+$\frac{1}{(3+2)(3+1)}$+…+$\frac{1}{(2017+2)(2017+1)}$
=$\frac{1}{1}$-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2018}$-$\frac{1}{2019}$
=1-$\frac{1}{2019}$
=$\frac{2018}{2019}$
点评 本题考查学生计算能力以及观察能力,解题的关键是求出a与b的值,以及恒等式$\frac{1}{(n+2)(n+1)}$=$\frac{(n+2)-(n+1)}{(n+2)(n+1)}$=$\frac{1}{n+1}$-$\frac{1}{n+2}$,本题属于中等题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
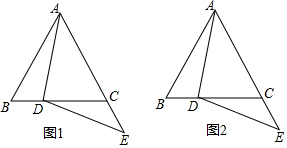 在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)
在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com