
【题目】如图,Rt△ABC中,∠ACB=90°,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
(1)证明:△AC C′∽△AB B′;
(2)设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时AC=BF,并说明理由.
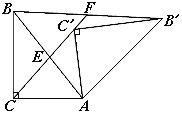
【答案】(1)证明见解析;(2)β=2α时AC=BF.
【解析】
(1)Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,可得AC=AC′,AB=AB′,∠CA C′=∠B AB′,再根据![]() ,即可证明△AC C′∽△AB B′;(2)欲证AC=BF,需证△AEC≌△FEB,则需证BE=CE,由已知可证∠BCE=∠ABC=a,即β=2α时,△AEC≌△FEB,故得证.
,即可证明△AC C′∽△AB B′;(2)欲证AC=BF,需证△AEC≌△FEB,则需证BE=CE,由已知可证∠BCE=∠ABC=a,即β=2α时,△AEC≌△FEB,故得证.
解:(1)证明:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的
∴AC=AC′,AB=AB′,∠CA C′=∠B AB′
∴![]()
∴△AC C′∽△AB B′
(2)当β=2α时AC=BF
证明:∵AC=AC′
∴∠AC C′=∠A C′C=![]() (180°-∠C AC′)=90°-
(180°-∠C AC′)=90°-![]() β=90°-α
β=90°-α
∵∠BCE=∠ACB-∠A C C′=90°-(90°-α)=α
∴∠BCE=∠ABC
∴BE=CE
∵∠ACE=∠ABF,∠AEC=∠FEB
∴△AEC≌△FEB
∴AC=BF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
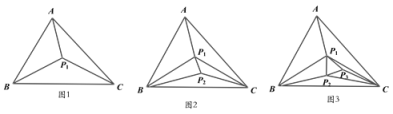
【题目】(问题背景)在△ABC内部,有地点![]() ,可构成3个不重叠的小三角形(如图1)
,可构成3个不重叠的小三角形(如图1)
(探究发现)当△ABC内的点的个数增加时,若其他条件不变,探究三角形内互不重叠的小三角形的个数情况。
(1)填表:
三角形内点的个数n | 1 | 2 | 3 | 4 | …… |
不重叠三角形个数S | …… |
(2)当△ABC内部有2019个点(![]() ,
,![]() ……
……![]() )时,三角形内不重叠的小三角形的个数S为多少?
)时,三角形内不重叠的小三角形的个数S为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(a+b)x+ab-1=0,x1、x2是此方程的两个实数根,现给出三个结论:①x1≠x2;②x1x2<ab;③![]() +
+![]() <a2+b2.则正确结论的序号是______.(填上你认为正确的所有序号)
<a2+b2.则正确结论的序号是______.(填上你认为正确的所有序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量白塔的高度AB,在D处用高为1.5米的测角仪 CD,测得塔顶A的仰角为42°,再向白塔方向前进12米,又测得白塔的顶端A的仰角为61°,求白塔的高度AB.(参考数据sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80,结果保留整数)
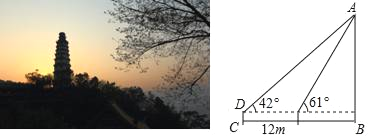
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行了“校园好声音”演唱比赛活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.

根据图中提供的信息,回答下列问题:
(1)求参加演唱比赛的学生共有多少人,并把条形图补充完整;
(2)求出扇形统计图中,m= ,n= ;
(3)求出C等级对应扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
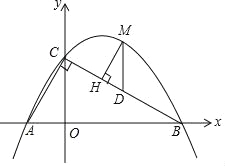
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个透明的布袋里装有2个红球,![]() 个白球,它们除颜色外其余都相同,已知任意摸出1个球是红球的概率为
个白球,它们除颜色外其余都相同,已知任意摸出1个球是红球的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)先任意摸出1个球,记下颜色后不放回,搅匀,再摸出一个球,请利用画树状图或列表的方法求出连续两次都摸出红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com