
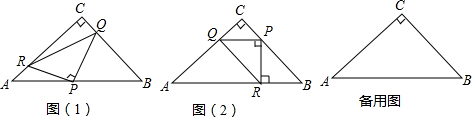
分析 (1)先判断出点C,R,P,Q四点共圆,得出∠ACP=∠BCP即可得出结论;
(2)①先设出PC=a,再用等腰直角三角形的性质表示出BC=3a,最后用三角形的面积公式即可得出结论;
②先设出PQ=PR=x,再用锐角三角函数表示出BC,最后用三角形的面积公式即可得出结论.
解答 解:(1)连接PC,
∵PQR是等腰直角三角形,
∴∠PQR=45°,
∵∠ACB=∠RPQ=90°.
∴点C,R,P,Q四点共圆,
∴∠ACP=∠PQR=45°,
∵∠ACB=90°,
∴∠ACP=∠BCP=45°,
∵AC=BC,
∴点P是AB的中点;
(2)①∵PR⊥AB,PR⊥PQ,
∴PQ∥AB,
设PC=a,在等腰直角三角形PCQ中,PQ=$\sqrt{2}$a,
∴PR=$\sqrt{2}$a,
在等腰直角三角形PBR中,PB=$\sqrt{2}$PR=2a,
∴BC=3a,
∴$\frac{{S}_{△PQR}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}P{Q}^{2}}{\frac{1}{2}{BC}^{2}}$=$\frac{(\sqrt{2}a)^{2}}{(3a)^{2}}$=$\frac{2}{9}$,
故答案为$\frac{2}{9}$;
②如图,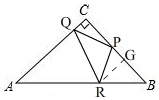
设PQ=PR=x,∠PQC=α(0°<α<90°),
在Rt△PCQ中,PC=PQ•sinα=x•sinα,
过点R作RG⊥BC,
在Rt△PGR中,PG=PR•cosα=x•cosα,RG=PR•sinα=x•sinα,
∴BG=RG=x•sinα,
∴BC=PC+PG+BG=x•sinα+x•cosα+x•sinαα=x(2sinα+cosα),
∴$\frac{{S}_{△PQR}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}P{Q}^{2}}{\frac{1}{2}B{C}^{2}}$=($\frac{1}{2sinα+cosα}$)2,
∵2sinα+cosα最大值为$\sqrt{5}$,
∴$\frac{{S}_{△PQR}}{{S}_{△ABC}}$的最小值为$\frac{1}{5}$.
点评 此题是三角形综合题,主要考查了四点共圆,等腰直角三角形的性质和判定,锐角三角函数,三角形的面积公式,解(1)的关键是判断出点C,R,P,Q四点共圆,解(2)的关键是设出等腰直角三角形PQR的直角边,表示出等腰直角三角形ABC的直角边,是一道难度比较大的中考题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,经过点A(0,6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0)、C两点.
如图,经过点A(0,6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0)、C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,点E、F分别是BC,AD上的点,且BE=DF,对角线AC⊥AB.
如图,在?ABCD中,点E、F分别是BC,AD上的点,且BE=DF,对角线AC⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com