
【题目】嘉嘉和琪琪在用一副三角尺研究数学问题:
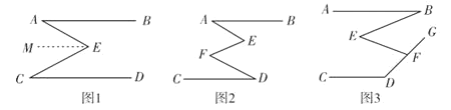
一副三角尺分别有一个角为直角,其余角度如图1所示,![]() .
.
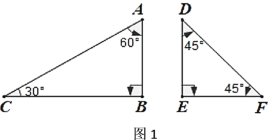
发现:
(1)如图2,当![]() 与
与![]() 重合时,
重合时,![]() _____.
_____.
(2)如图3,将图2中![]() 绕
绕![]() 点顺时针旋转一定角度使得
点顺时针旋转一定角度使得![]() ,求
,求![]() 的度数.
的度数.
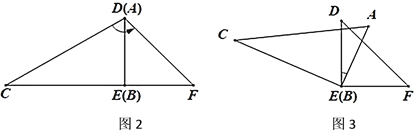
拓展:
(3)如图4,继续旋转,使得![]() 于点
于点![]() ,
,
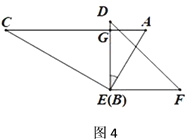
①此时![]() 与
与![]() 平行吗?请说明理由.
平行吗?请说明理由.
②求![]() 的度数.
的度数.
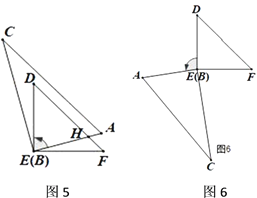
探究:
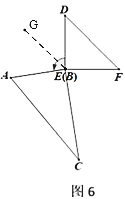
(4)如图5、图6,继续旋转,使得![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①平行,垂直于同一条直线的两条直线平行;②
;(3)①平行,垂直于同一条直线的两条直线平行;②![]() ;(4)
;(4)![]() ,
,![]() ;
;
【解析】
(1)利用角的和差关系计算即可;(2)利用角的和差关系计算即可;(3)①根据平行线的判定定理即可得答案;②利用直角三角形两锐角互余的性质即可得答案;(4)在图5中,根据平行线的性质可得∠DHE的度数,根据三角形内角和定理即可求出∠AED的度数,在图6中,过E作EG//AC,根据平行线的性质即可得∠AED的度数.
(1)∵∠CAB=60°,∠EDF=45°,
∴∠CDF=∠CAB+∠EDF=105°,
(2)∵![]() ,∠CBA=90°,∠DEF=90°,
,∠CBA=90°,∠DEF=90°,
∴∠CBA+∠AEB=∠CBA+∠DEF-∠AED=90°+90°-∠AED=156°,
∴∠AED=180°-156°=24°.
(3)①平行,理由如下:
∵![]() ,∠DEF=90°,
,∠DEF=90°,
∴AC//EF.
②∵![]() ,∠C=30°,
,∠C=30°,
∴∠CED=90°-30°=60°,
∵∠CBA=90°,
∴∠AED=90°-60°=30°,
(4)在图5中,
∵AC//EF,
∴∠DHE=∠A=60°,
∵∠D=45°,
∴∠AED=180°-60°-45°=75°,
在图6中,过过E作EG//AC,
∵AC//DF,EG//AC,
∴EG//DF,
∴∠DEG=∠D=45°,∠AEG=∠A=60°,
∴∠AED=45°+60°=105°,


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠A=30°,∠C=40°,求∠AEC的度数.小明的思路是:

(1)初步尝试:按小明的思路,求得∠AEC的度数;
(2)问题迁移:如图2,AB∥CD,点E、F为AB、CD内部两点,问∠A、∠E、∠F和∠D之间有何数量关系?请说明理由;
(3)应用拓展:如图3,AB∥CD,点E、F为AB、CD内部两点,如果∠E+∠EFG=160°,请直接写出∠B与∠D之问的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准,共支付两种垃圾处理费5000元,从去年元月起,收费标准上调为:可回收垃圾处理费30元/吨,不可回收垃圾处理费100元/吨.若该企业去年处理的这两种垃圾数量与前年相比没有变化,但调价后就要多支付处理费9000元.
(1)该企业前年处理的可回收垃圾和不可回收垃圾各多少吨?
(2)该企业计划今年将上述两种垃圾处理总量减少到200吨,且可回收垃圾不少于不可回收垃圾处理量的3倍,则今年该企业至少有多少吨可回收垃圾?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界上大部分国家都使用摄氏温度(![]() ),但美国、英国等国家的天气预报仍然使用华氏温度(
),但美国、英国等国家的天气预报仍然使用华氏温度(![]() ).两种计量之间有如下对应:
).两种计量之间有如下对应:
摄氏温度( |
|
|
|
|
|
|
华氏温度( |
|
|
|
|
|
|
(1)上表反映了哪两变量之间的关系?哪个是自变量?哪个是因变量?
(2)由上表可得:摄氏温度(![]() )每提高
)每提高![]() 度,华氏温度(
度,华氏温度(![]() )提高_____度.
)提高_____度.
(3)摄氏温度![]() 度时华氏温度为______度.
度时华氏温度为______度.
(4)华氏温度![]() 度时摄氏温度为_______度.
度时摄氏温度为_______度.
(5)华氏温度的值与对应的摄氏温度的值有相等的可能吗?如果有,求出这个值.如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3米,探测线与地面的夹角分别是30°和60°(如图),试确定生命所在点C的深度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开展全科大阅读活动,学校花费了3400元在书店购买了40套古典文学书籍和20套现代文学书籍,每套现代文学书籍比每套古典文学书籍多花20元.
(1)求每套古典文学习书籍和现代文学书籍分别是多少元?
(2)为满足学生的阅读需求,学校计划用不超过2500元再次购买古典文学和现代文学书籍共40套,经市场调查得知,每套古典文学书籍价格上浮了20%,每套现代文学书籍价格下调了10%,学校最多能购买多少套现代文学书籍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题再现:
数形结合是一种重要的数学思想方法,借助这种思想方法可将抽象的数学知识变得直观并且具有可操作性.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义验证完全平方公式.
将一个边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
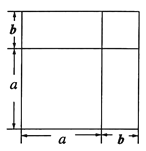
![]() 或
或![]()
∴![]()
这就验证了两数和的完全平方公式.
类比解决:
请你类比上述方法,利用图形的几何意义验证平方差公式.
(要求画出图形并写出推理过程)
问题提出:如何利用图形几何意义的方法证明![]() ?
?
如图所示,![]() 表示1个1×1的正方形,即:
表示1个1×1的正方形,即:![]() ,
,![]() 表示1个2×2的正方形,
表示1个2×2的正方形,![]() 与
与![]() 恰好可以拼成1个2×2的正方形,因此:
恰好可以拼成1个2×2的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2个2×2的正方形,即:
就可以表示2个2×2的正方形,即:![]() 而
而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一个
恰好可以拼成一个![]() 的大正方形.
的大正方形.
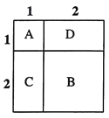
由此可得:![]() .
.
尝试解决:
请你类比上述推导过程,利用图形的几何意义确定:![]() _______.(要求写出结论并构造图形写出推证过程).
_______.(要求写出结论并构造图形写出推证过程).
问题拓广:
请用上面的表示几何图形面积的方法探究:![]() _______.(直接写出结论即可,不必写出解题过程).
_______.(直接写出结论即可,不必写出解题过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com