
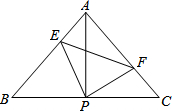
 ��֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F�������������ĸ����ۣ�
��֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F�������������ĸ����ۣ�| A�� | �٢� | B�� | �٢� | C�� | �٢ڢ� | D�� | �٢ڢۢ� |
���� ���ݵ���ֱ�������ε����ʵã�AP��BC��AP=$\frac{1}{2}$BC��APƽ�֡�BAC�����Կ�֤��C=��EAP����FPC=��EPA��AP=PC����֤�á�APE���CPFȫ�ȣ�����ȫ�������������жϽ����Ƿ���ȷ��
��� �⣺�ߡ�APE����CPF���ǡ�APF����ǣ�
���APE=��CPF��
��AB=AC����BAC=90�㣬P��BC�е㣬
��AP=CP��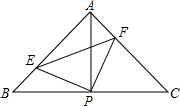
���PAE=��PCF��
�ڡ�APE���CPF�У�
$\left\{\begin{array}{l}{��PAE=��PCF}\\{AP=CP}\\{��EPA=��FPC}\end{array}\right.$��
���APE�ա�CPF��ASA����
ͬ����֤��APF�ա�BPE��
��AE=CF����EPF�ǵ���ֱ�������Σ�S�ı���AEPF=$\frac{1}{2}$S��ABC���٢ڢ���ȷ��
��AP=$\frac{1}{2}$BC����EF���ǡ�ABC����λ��ʱ����EF������BC��һ�룬EF=AP��
��ʢܲ�������
��ʼ����ȷ���Ǣ٢ڢۣ�
��ѡ��C��
���� ������Ҫ�����˵���ֱ�������ε��ж������ʵ����ã������ε���λ�ߵ����ʵ����ã�ȫ�������ε��ж������ʵ����ã����ʱ֤��������ȫ���ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ijУ����ĩ��֯ʦ���ιۺ����ң����м���������������շ�y����y����x��xΪ�ι��������ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ���ش��������⣺
��ͼ��ijУ����ĩ��֯ʦ���ιۺ����ң����м���������������շ�y����y����x��xΪ�ι��������ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ���ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
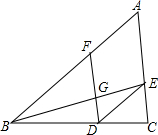 ��ͼ���ڡ�ABC�У���D��E��F�ֱ��ڱ�BC��AC��AB�ϣ�����BE��DF���ڵ�G������DE�����ı���AFDE��ƽ���ı��Σ�������˵��������ǣ�������
��ͼ���ڡ�ABC�У���D��E��F�ֱ��ڱ�BC��AC��AB�ϣ�����BE��DF���ڵ�G������DE�����ı���AFDE��ƽ���ı��Σ�������˵��������ǣ�������| A�� | $\frac{AF}{AB}$=$\frac{EG}{BE}$ | B�� | $\frac{FG}{GD}$=$\frac{BG}{GE}$ | C�� | $\frac{FG}{AE}$=$\frac{DG}{EC}$ | D�� | $\frac{AF}{BF}$=$\frac{AE}{EC}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M��N | B�� | M=N | C�� | M��N | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com