
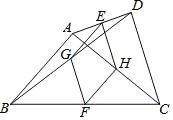
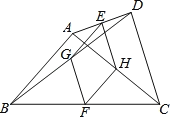
【题目】如图,在四边形ABCD中,AB=CD,E、F、G、H分别为AD、BC、BD、AC的中点,顺次连接E、G、F、H.
(1)猜想四边形EGFH是什么特殊的四边形,并说明理由;
(2)当∠ABC与∠DCB满足什么关系时,四边形EGFH为正方形,并说明理由;
(3)猜想:∠GFH、∠ABC、∠DCB三个角之间的关系.直接写出结果____________.
【答案】(1)菱形;(2)∠ABC+∠DCB=90°;(3)∠GFH+∠ABC+∠DCB=180°或∠GFH+∠ABC-∠DCB=180°
【解析】
(1)根据三角形中位线的性质得到EG![]() AB,EH
AB,EH![]() CD,HF
CD,HF![]() AB,EG∥AB,HF∥AB,根据菱形的判定定理即可得到结论;
AB,EG∥AB,HF∥AB,根据菱形的判定定理即可得到结论;
(2)根据平行线的性质得到∠ABC=∠HFC,∠DCB=∠GFB,根据平角的定义得到∠GFH=90°,于是得到结论;
(3)由平行线的性质得到∠ABC=∠HFC,∠DCB=∠GFB,根据平角的定义即可得到结论.
(1)四边形EGFH是菱形.理由如下:
∵E、F、G、H分别为AD、BC、BD、AC的中点,
∴EG![]() AB,EH
AB,EH![]() CD,HF
CD,HF![]() AB,EG∥AB,HF∥AB,
AB,EG∥AB,HF∥AB,
∴四边形EGFH是平行四边形,EG=EH,
∴四边形EGFH是菱形;
(2)当∠ABC+∠DCB=90°时,四边形EGFH为正方形,
理由:∵GF∥CD,HF∥AB,
∴∠ABC=∠HFC,∠DCB=∠GFB.
∵∠ABC+∠DCB=90°,
∴∠GFH=90°,
∴菱形EGFH是正方形;
(3)当∠ABC+∠DCB<180°时,∠GFH+∠ABC+∠DCB=180°.
理由如下:
∵GF∥CD,HF∥AB,
∴∠ABC=∠HFC,∠DCB=∠GFB.
∵∠BFG+∠GFH+∠HFC=180°,
∴∠GFH+∠ABC+∠DCB=180°.
当∠ABC+∠DCB=180°时,∠GFH=0°,四边形EGFH不存在,∠GFH+∠ABC+∠DCB=180°;
当∠ABC+∠DCB>180°时,∠GFH+∠ABC﹣∠DCB=180°.
综上所述:∠GFH+∠ABC+∠DCB=180°或∠GFH+∠ABC-∠DCB=180°.


科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,第n次操作后,得到△AnBnCn,要使△AnBnCn的面积超过2020,则至少需要操作__________次.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:我们把只有一组对角是直角的四边形叫做准矩形.
(1)图①、图②均为3×3的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.线段AB、BC的端点均在格点上,在图①、图②中各画一个准矩形ABCD,要求:准矩形ABCD的顶点D在格点上,且两个准矩形不全等.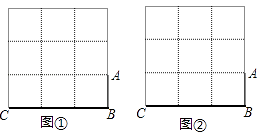
(2)如图③,正方形ABCD的边长为4,准矩形ABMN的顶点M、N分别在正方形ABCD的边上.若准矩形ABMN的一条对角线长为5,直接写出此时该准矩形的面积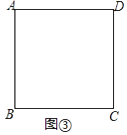
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成证明并写出推理根据:如图,直线![]() 分别与直线
分别与直线![]() 、
、![]() 交于点
交于点![]() 和点
和点![]() ,
,![]() ,射线
,射线![]() 、
、![]() 分别与直线
分别与直线![]() 交于点
交于点![]() 、
、![]() ,且
,且![]() ,则
,则![]() 与
与![]() 有何数量关系?并说明理由.
有何数量关系?并说明理由.

解:![]() 与
与![]() 的数量关系为 ① ,理由如下:
的数量关系为 ① ,理由如下:
∵![]() (已知)
(已知)
∴ ② // ② ( ② )
∴![]() ③ ( ③ )
③ ( ③ )
∵![]() (已知)
(已知)
∴ ④ ( ④ )
∵![]() ⑤
⑤
∴![]() ⑥ -
⑥ -![]() ⑥
⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )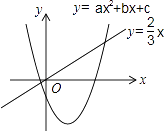
A.大于0
B.等于0
C.小于0
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表.
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,求工厂的最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名射击选手中选出一名选手参加省级比赛,现对他们分别进行5次射击测试,成绩分别为(单位:环)甲:5、6、7、9、8;乙:8、4、8、6、9,
(1)甲运动员5次射击成绩的中位数为________环,极差是________环;乙运动员射击成绩的众数为________环.
(2)已知甲的5次成绩的方差为2,通过计算,判断甲、乙两名运动员谁的成绩更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
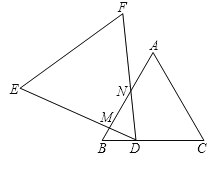
【题目】将两个等边△ABC和△DEF(DE>AB)如图所示摆放,点D是BC上的一点(除B、C点外).把△DEF绕顶点D顺时针旋转一定的角度,使得边DE、DF与△ABC的边(除BC边外)分别相交于点M、N.
(1)∠BMD和∠CDN相等吗?
(2)画出使∠BMD和∠CDN相等的所有情况的图形.
(3)在(2)题中任选一种图形说明∠BMD和∠CDN相等的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com