
【题目】已知,如图,EB是![]() 的直径,且
的直径,且![]() ,在BE的延长线上取点P,使
,在BE的延长线上取点P,使![]() ,A是EP上一点,过A作
,A是EP上一点,过A作![]() 的切线,切点为D,过D作
的切线,切点为D,过D作![]() 于F,过B作AD的垂线BH,交AD的延长线于
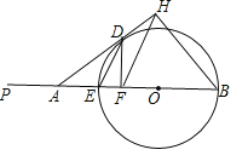
于F,过B作AD的垂线BH,交AD的延长线于![]() 当点A在EP上运动,不与E重合时:
当点A在EP上运动,不与E重合时:
![]() 是否总有
是否总有![]() ,试证明你的结论;
,试证明你的结论;
![]() 设
设![]() ,
,![]() ,求y和x的函数关系,并写出x的取值范围.
,求y和x的函数关系,并写出x的取值范围.
【答案】(1)有,理由见解析;(2)![]()
【解析】
(1) 连接BD,先证△DFB≌△DHB,由此可得△BFH是等腰三角形,根据等腰三角形三线合一的性质可证得BD⊥FH,而BD⊥DE,则FH∥DE,由此得证.
(2) 由于BH=BF,可用y表示出EF的值,进而在Rt△DEB中,根据射影定理得到y、x的函数关系式;当A、P重合时,连接OD,则OD⊥PH,根据平行线分线段成比例,可求得BH的长,进而可得到BF、EF的值,然后由射影定理即可求得DE的长,求得x的取值范围.
解:(1)无论点A在EP上怎么移动![]() 点A不与点E重合
点A不与点E重合![]() ,
,
总有![]() ,证明如下:
,证明如下:
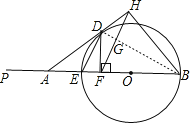
连接DB,交FH于G,如下图所示:
![]() 是
是![]() 的切线,
的切线,![]() .
.
又![]() ,BE为直径,
,BE为直径,
![]() .有
.有![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ≌
≌![]() .
.
∴![]()
∴![]() 是等腰三角形.
是等腰三角形.
∴![]() ,即
,即![]() .
.
![]() ,
,
![]() .
.
故答案为:总有![]() 成立.
成立.
(2)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
又![]() 是
是![]() 斜边上的高,
斜边上的高,
![]() ∽
∽![]() ,
,
![]() ,
,
即![]() .
.![]() 即
即![]() ,
,
![]() ,
,
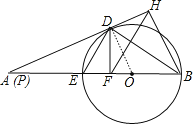
当A从E向左移动,ED逐渐增大,当A和P重合时,ED最大,
这时,连接OD,如下图所示:
则![]() ,
,
![]() .
.
又![]() ,
,![]() ,
,
![]() ,即:
,即:![]() ,
,
![]() ,
,![]() .
.
由![]() ,
,
得:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
故答案为:所求函数关系式为![]()


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
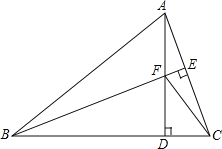
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,CD=![]() ,AD与BE交于点F,连接CF,则AD的长为_____.
,AD与BE交于点F,连接CF,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
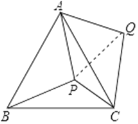
【题目】P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0,x>0)的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),
(m≠0,x>0)的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),![]() =
=![]() .
.
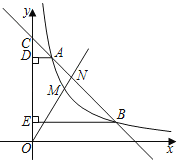
(1)求m的值和一次函数的解析式;
(2)若点M为反比例函数图象在A,B之间的动点,作射线OM交直线AB于点N,当MN长度最大时,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
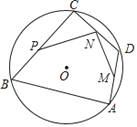
【题目】如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为![]() 上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
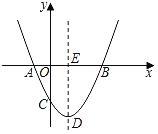
【题目】如图,抛物线y=ax2+bx+c的顶点为D,与x轴交点A,B的横坐标分别为﹣1,3,与y轴负半轴交于点C.下面五个结论:
①2a+b=0;
②4a+2b+c>0;
③对任意实数x,ax2+bx≥a+b;
④只有当a=![]() 时,△ABD是等腰直角三角形;
时,△ABD是等腰直角三角形;
⑤使△ABC为等腰三角形的a值可以有3个.
其中正确的结论有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
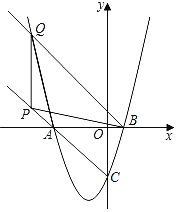
【题目】如图,抛物线y=x2﹣ax+a﹣1与x轴交于A,B两点(点B在正半轴上),与y轴交于点C,OA=3OB.点P在CA的延长线上,点Q在第二象限抛物线上,S△PBQ=S△ABQ.
(1)求抛物线的解析式.
(2)求直线BQ的解析式.
(3)若∠PAQ=∠APB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
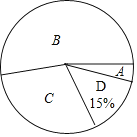
【题目】某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
合计 | 100 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
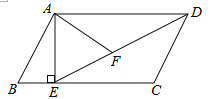
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)在图中找出一对相似三角形,并说明理由;
(2)若AB=8,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com